Princípio Fundamental da Contagem
Lista de 10 exercícios de Matemática com gabarito sobre o tema Princípio Fundamental da Contagem com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Princípio Fundamental da Contagem.
01. (ESPM) Uma sequência de números naturais é obtida de modo que, se um número é par, o próximo será sua metade mas, se for ímpar, o próximo será uma unidade a mais que ele, até chegar no número 1. Por exemplo: S(42) = (42, 21, 22, 11, 12, 6, 3, 4, 2, 1) O número de termos dessa sequência é igual a 10.
Podemos afirmar que a quantidade de sequências assim definidas e com exatamente 7 termos é igual a:
- 6
- 7
- 8
- 9
- 10
02. (UEG) Uma montadora de carros oferece a seus clientes as seguintes opções na montagem de um carro: 2 tipos de motores (1.8 ou 2.0), 2 tipos de câmbios (manual ou automático), 6 cores (branco, preto, vermelho, azul, cinza ou prata) e 3 tipos de acabamento (simples, intermediário ou sofisticado). De quantas maneiras distintas pode-se montar esse carro?
- 4
- 13
- 24
- 36
- 72
03. (UEG) Numa lanchonete o lanche é composto por três partes: pão, molho e recheio. Se essa lanchonete oferece aos seus clientes duas opções de pão, três de molho e quatro de recheio, a quantidade de lanches distintos que ela pode oferecer é de
- 9
- 12
- 18
- 24
04. (UEMG) “Genius era um brinquedo muito popular na década de 1980 (...). O brinquedo buscava estimular a memorização de cores e sons. Com formato semelhante a um OVNI, possuía 4 botões de cores distintas que emitiam sons harmônicos e se iluminavam em sequência. Cabia aos jogadores repetir o processo sem errar”.
Considerando uma fase do jogo em que 3 luzes irão acender de forma aleatória e em sequência, podendo cada cor acender mais de uma vez.
O número máximo de formas que essa sequência de 3 luzes poderá acender é:

- 12.
- 24.
- 36.
- 64.
05. (PUC-SP) Uma pessoa dispõe das seguintes cores de tinta: amarela, azul, verde, vermelha e branca, e irá utilizá-las para pintar um pote. Nesse pote serão pintadas a tampa, a lateral e uma lista na lateral, de modo que a tampa e a lateral poderão ter a mesma cor ou cores diferentes. O número de maneiras distintas de pintar esse pote é
- 100
- 80
- 60
- 40
06. (UECE) Quantos números inteiros positivos pares, com três dígitos distintos, podemos formar com os algarismos 3, 4, 5, 6 e 7?
- 28.
- 36.
- 32.
- 24.
07. (EEAR) Considere os algarismos 1, 2, 3, 4, 5, e 6. A partir deles, podem ser criados ____ números pares de quatro algarismos distintos.
- 60
- 120
- 180
- 360
08. (UECE) No sistema de numeração decimal, quantos números de três dígitos distintos podemos formar, de modo que a soma dos dígitos de cada um destes números é um número impar?
- 420.
- 380.
- 360.
- 320.
09. (AFA) Um baralho é composto por 52 cartas divididas em 4 naipes distintos (copas, paus, ouros e espadas). Cada naipe é constituído por 13 cartas, das quais 9 são numeradas de 2 a 10, e as outras 4 são 1 valete (J), 1 dama (Q), 1 rei (K) e 1 ás (A).
Ao serem retiradas desse baralho duas cartas, uma a uma e sem reposição, a quantidade de sequências que se pode obter em que a primeira carta seja de ouros e a segunda não seja um ás é igual a:
- 612
- 613
- 614
- 615
10. (IFAL) Em uma civilização antiga, o alfabeto tinha apenas três letras. Na linguagem dessa civilização, as palavras tinham de uma a quatro letras. Quantas palavras existiam na linguagem dessa civilização?
- 4.
- 12.
- 16.
- 40.
- 120.
11. (FAMEMA) Uma pessoa dispõe de 5 blocos de papel colorido nas cores azul, amarelo, verde, branco e rosa, sendo cada um deles de uma única cor, e irá utilizar 3 folhas para anotações. O número total de maneiras possíveis de essa pessoa escolher essas 3 folhas, sendo pelo menos 2 delas de uma mesma cor, é
- 22.
- 12.
- 15.
- 18.
- 25.
12. (UFRGS) Uma caixa contém 32 esferas numeradas de 1 a 32. O número de maneiras distintas de retirar 3 esferas da caixa, ordenadas como primeira, segunda e terceira, em que a esfera com o número 8 seja pelo menos a terceira a ser retirada é
- 27.
- 96.
- 2000.
- 2018.
- 2790.
13. (Mackenzie) Cada um dos círculos da figura deverá ser pintado com uma cor, escolhida dentre três disponíveis.
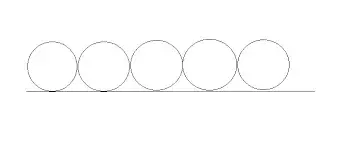
Sabendo que dois círculos consecutivos nunca serão pintados com a mesma cor, o número de formas de se pintar os círculos é
- 72
- 68
- 60
- 54
- 48
14. (PUC-SP) Na sala de reuniões de certa empresa há uma mesa retangular com 10 poltronas dispostas da forma como é mostrado na figura abaixo.

Certo dia, sete pessoas foram convocadas para participar de uma reunião a ser realizada nessa sala: o presidente, o vice-presidente, um secretário e quatro membros da diretoria. Sabe-se que:
• o presidente e o vice-presidente deverão ocupar exclusivamente as poltronas das cabeceiras da mesa;
• o secretário deverá ocupar uma poltrona ao lado do presidente. Considerando que tais poltronas são fixas no piso da sala, de quantos modos as sete pessoas podem nelas se acomodar para participar de tal reunião?
- 3360
- 2480
- 1680
- 1240
- 840
15. (UFMG) Observe o diagrama.
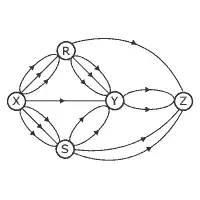
Qual é o numero de ligações distintas entre X e Z
- 39
- 41
- 35
- 45