Matrizes

1. (UEL-PR) Sabendo-se que a matriz

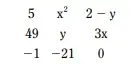
é igual à sua transposta, o valor de x.2y é:

1. -20
2. -1
3. 1
4. 13
5. 20

2. (UDESC) Sendo a matriz igual à matriz identidade de ordem 2, o valor de 2.x é:

1. – 4
2. 6
3. 4
4. 8
5. – 8

3. (Unicamp) Sejam a e b números reais tais que a matriz A satisfaz a equação A2= aA + bI, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a

1. −2.
2. −1.
3. 1.
4. 2.

4. (Unesp) Considere a equação matricial A + BX = X + 2C, cuja incógnita é a matriz X e todas as matrizes são quadradas de ordem n. A condição necessária e suficiente para que esta equação tenha solução única é que:

1. B – I ≠ O, onde I é a matriz identidade de ordem n e O é a matriz nula de ordem n.
2. B seja invertível.
3. B ≠ O, onde O é a matriz nula de ordem n.
4. B – I seja invertível, onde I é a matriz identidade de ordem n.
5. A e C sejam invertíveis.

5. (UFPR) Dados os números reais a, b e c diferentes de zero e a matriz quadrada de ordem 2

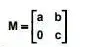
considere as seguintes afirmativas a respeito de M:

1. A matriz M é invertível.

2. Denotando a matriz transposta de M por M^T, teremos det(M.M^T) > 0.

3. Quando a = 1 e c = −1 , tem-se M² = I, sendo I a matriz identidade de ordem 2.

Assinale a alternativa correta.

1. Somente a afirmativa 2 é verdadeira.
2. Somente a afirmativa 3 é verdadeira.
3. Somente as afirmativas 1 e 2 são verdadeiras.
4. Somente as afirmativas 2 e 3 são verdadeiras.
5. As afirmativas 1, 2 e 3 são verdadeiras.

6. (Unicamp) Em uma matriz, chamam-se elementos internos aqueles que não pertencem à primeira nem à última linha ou coluna. O número de elementos internos em uma matriz com 5 linhas e 6 colunas é igual a:

1. 12.
2. 15.
3. 16.
4. 20.

7. (Unicamp) Considere a matriz quadrada de ordem 3, onde x é um número real.

Podemos afirmar que:

1. A não é invertível para nenhum valor de x .
2. A é invertível para um único valor de x .
3. A é invertível para exatamente dois valores de x .
4. A é invertível para todos os valores de x .

8. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:

1. existe A + B se, e somente se, n = 4 e m = 3;
2. existe AB se, e somente se, n = 4 e m = 3;
3. existem AB e BA se, e somente se, n = 4 e m = 3;
4. existem, iguais, A + B e B + A se, e somente se, A = B;
5. existem, iguais, AB e BA se, e somente se, A = B.

9. (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:

1. (A = B) . C = A . C + B . C
2. (A + B)^t = A^t + B^t
3. (A . B)^t = A^t . B^t
4. (A – B)C = AC – BC
5. (A^t)^t = A

10. (UFU) Considere a matriz:

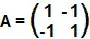
Então A⁴ + 2A³ + 4A² + 8A é igual a:

1. A⁶
2. A⁸
3. A¹⁰
4. A⁵