Volume da Pirâmide

01. (EEAR) Uma pirâmide quadrangular regular tem 260 cm² de área lateral e 13 cm de apótema.

Assim, o volume dessa pirâmide é______cm³.

1. 100
2. 200
3. 300
4. 400

1. 2cm
2. 4cm
3. 6cm
4. 8cm
5. 10cm

03. (UERJ) Observe a seguir a imagem de uma pirâmide quadrangular regular e a planificação de sua superfície total. Na planificação, o ponto A representa um vértice de uma face lateral e o ponto B o centro da base, sendo AB = 16 cm.

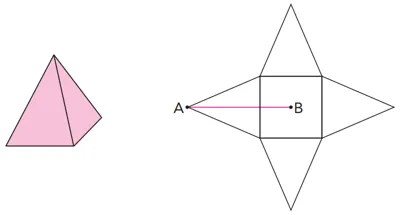
Se a aresta da base dessa pirâmide mede 12 cm, seu volume, em cm³, é igual a:

1. 384
2. 376
3. 364
4. 356

04. (UNESP) A figura indica o projeto de uma escultura maciça em forma de pirâmide de vértice V, base ABCDEFGH e altura VH, que será feita com espuma expansiva rígida de poliuretano. Sabe-se que AHGF é um quadrado de área igual a 3 m², BCDE é um retângulo, com BC = 3 m e CD = 4, e que o ângulo HGV mede 60º.

Sabendo que 1 m³ corresponde a 1000 litros e que o custo da quantidade de espuma de poliuretano necessária para ocupar a capacidade de 1 litro é de R$ 5,00, para fazer por completo essa escultura, desconsiderando desperdícios, o valor gasto com espuma será de

1. R$ 40.000,00.
2. R$ 37.500,00.
3. R$ 42.500,00.
4. R$ 35.000,00.
5. R$ 45.000,00.

05. (UERJ) Um recipiente com a forma de uma pirâmide de base quadrada foi completamente preenchido com um líquido. Sua aresta da base mede 4 cm e a altura, 9 cm. Em seguida, todo esse líquido foi transferido para outro recipiente, com a forma de um prisma reto, sendo sua base um triângulo retângulo isósceles cujos catetos medem 4 cm. Observe as imagens:

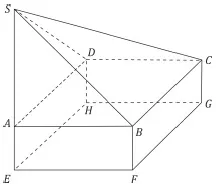
Considere que as espessuras dos recipientes são desprezíveis e que as bases estão em planos horizontais, sendo as alturas definidas em relação às bases.

A altura h, em centímetros, que o líquido atingirá no segundo recipiente é:

1. 10
2. 8
3. 6
4. 4

06. (ITA) Uma esfera está inscrita em uma pirâmide regular hexagonal cuja altura mede 12 cm e a aresta da base mede 10/3 √3 cm. Então o raio da esfera, em cm, é igual a

1. 10/3√3
2. 13/3
3. 15/4
4. 2√3
5. 10/3

07. (Fuvest) Uma pirâmide tem como base um quadrado de lado 1, e cada uma de suas faces laterais é um triângulo equilátero. Então, a área do quadrado, que tem como vértices os baricentros de cada uma das faces laterais, é igual a

1. 5/9
2. 4/9
3. 1/3
4. 2/9
5. 1/9

08. (UFT) A pirâmide a seguir foi construída com cubos maciços de mesmas dimensões.

Considerando-se que, na construção da pirâmide não foram deixados espaços vazios em seu interior e que o volume de cada cubo é 1m³ , pode-se afirmar que o volume total e a altura desta pirâmide são, respectivamente:

1. 5m³ e 1m
2. 25m³ e 5m
3. 125m³ e 25m
4. 165m³ e 5m
5. 625m³ e 25m

09. (UNEB) Uma pirâmide é seccionada a uma distância de 2/3 de sua base.

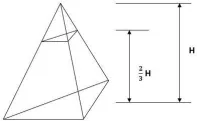
Sabendo que o volume dessa pirâmide é igual a 81 cm³ , calcule, em cm³ , o volume do tronco de pirâmide obtido a partir desse seccionamento.

1. 62
2. 70
3. 78
4. 67
5. 60

10. (UERJ) Observe na imagem uma pirâmide de base quadrada, seccionada por dois planos paralelos à base, um contendo o ponto A e o outro o ponto B. Esses planos dividem cada aresta lateral em três partes iguais.

Considere as seguintes medidas da pirâmide: • altura = 9 cm; • aresta da base = 6 cm; • volume total = 108 cm³.

O volume da região compreendida entre os planos paralelos, em cm³ , é:

1. 26
2. 24
3. 28
4. 30