Área da Pirâmide

01. (FATEC) Um artista plástico deseja construir uma obra chamada “A pirâmide da desigualdade da riqueza no Brasil”. Ele fará uma réplica do gráfico apresentado, mantendo todas as suas proporções.

Nesse gráfico, considere que a altura da pirâmide referente à riqueza dos 10% mais ricos seja 90% da altura da pirâmide total de distribuição de riqueza e que essas pirâmides sejam semelhantes entre si.

Para construir a obra, ele utilizará quatro triângulos isósceles congruentes entre si e um quadrado, todos feitos de metal, deixando o interior da pirâmide vazio. A pirâmide terá 4 metros de altura, e a base quadrada terá 6 metros de lado.

O total de metal necessário para construir essa obra será, em metros quadrados, igual a

Despreze a espessura das placas de metal.

1. 58
2. 60
3. 72
4. 84
5. 96

02. (Albert Einstein) Para a feira cultural da escola, um grupo de alunos irá construir uma pirâmide reta de base quadrada. A pirâmide terá 3 m de altura e cada aresta da base medirá 2 m. A lateral da pirâmide será coberta com folhas quadradas de papel, que poderão ser cortadas para um melhor acabamento. Se a medida do lado de cada folha é igual a 20 cm, o número mínimo dessas folhas necessárias à execução do trabalho será

Utilize √10 = 3,2

1. 285
2. 301
3. 320
4. 333

03. (ENEM PPL 2016) A figura mostra a pirâmide de Queops, também conhecida como a Grande Pirâmide. Esse e o monumento mais pesado que já foi construído pelo homem da Antiguidade. Possui aproximadamente 2,3 milhões de blocos de rocha, cada um pesando em média 2,5 toneladas. Considere que a pirâmide de Quéops seja regular, sua base seja um quadrado com lados medindo 214 m, as faces laterais sejam triângulos isósceles congruentes e suas arestas laterais meçam 204 m.

O valor mais aproximado para a altura da pirâmide de Quéops, em metro, é

1. 97,0.
2. 136,8.
3. 173,7.
4. 189,3.
5. 240,0.

04. (ESA) Em uma pirâmide reta de base quadrada, de 4 m de altura, uma aresta da base mede 6 m.

A área total dessa pirâmide, em m², é

1. 144
2. 84
3. 48
4. 72
5. 96

05. (PUC-Campinas) Considere dois troncos de pirâmides retas exatamente iguais. A base maior é um quadrado de lado igual a 2 metros, a base menor um quadrado de lado igual a 1 metro, e a distância entre as bases igual a 1 metro. Um monumento foi construído justapondo-se esses dois troncos nas bases menores, apoiando-se em um piso plano por meio de uma das bases maiores, formando um sólido. Desta maneira, a medida da área da superfície exposta do monumento é, em m², igual a

1. 4 + 6√5.
2. 8.
3. 12√2 + 4.
4. 16/3.
5. 12√2 − 8.

06. (UPE) Uma pirâmide quadrangular regular tem volume V = 36√7 centímetros cúbicos. Se a aresta da base mede 6 cm, qual é o valor aproximado de sua área total em cm²?

Considere √2 = 1,4

1. 105
2. 135
3. 137
4. 208
5. 214

07. (UFMS) Uma pirâmide reta tem base quadrada de área 196 cm².

Sabendo que a área de uma das faces laterais desse sólido é 175 cm², a altura dessa pirâmide é

1. 20 cm,
2. 21 cm.
3. 24 cm.
4. 25 cm.
5. 28 cm.

08. (Santa Casa) Um enfeite de Natal, em formato de pirâmide regular de base quadrada de 40 cm de lado, foi acomodado dentro de uma caixa em formato de prisma reto de base quadrada de lado medindo 40 cm e altura 80 cm, como mostra a figura.

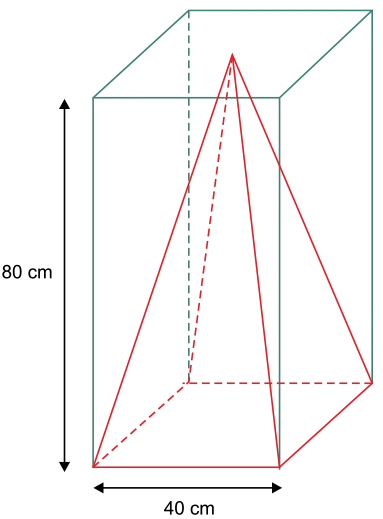
Admitindo-se que a pirâmide se encaixa perfeitamente, sem folga, na caixa, a área lateral da pirâmide é

1. 1580 √15 cm²
2. 1560 √13 cm²
3. 1600 √17 cm²
4. 1540 √11 cm²
5. 1520 √19 cm²

09. (UECE) Considere uma pirâmide regular hexagonal reta cuja medida da altura é 30 m e cuja base está inscrita em uma circunferência cuja medida do raio é igual a 10 m. Desejando-se pintar todas as faces triangulares dessa pirâmide, a medida da área a ser pintada, em m², é

1. 115. √39
2. 150.√39
3. 125. √39
4. 140. √39

10. (UECE) A base de uma pirâmide é uma das faces de um cubo cuja soma das medidas das áreas das faces é 1014 m².

Se o vértice da pirâmide é o centro do cubo, a medida da área lateral da pirâmide, em m² , é igual a

1. 169 √2/2.
2. 169 √2.
3. 169 √3/2.
4. 169 √3.