Área do Cilindro

01. (UNESP) O indicador de direção do vento, também conhecido como biruta, é item obrigatório em todo heliponto. Suas dimensões devem estar em conformidade com a figura e com a tabela apresentadas na sequência, retiradas do Regulamento Brasileiro da Aviação Civil.

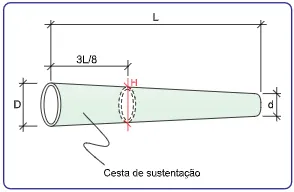
(Agência Nacional de Aviação Civil. RBAC no 155, 25.05.2018. Adaptado.)

A fabricação da cesta de sustentação é baseada nos valores de D, L e H e considera que a figura corresponde a um tronco de cone reto, cujas circunferências de diâmetros D, H e d são paralelas.

1. 52,50 cm.
2. 41,25 cm.
3. 48,75 cm.
4. 37,50 cm.
5. 45,00 cm.

02. (UEA) Um sólido, no formato de um cilindro circular reto, tem volume igual a 54π cm3, e sua área lateral (AL) é calculada pela expressão AL = 2π ⋅ R ⋅ H, em que R e H são, respectivamente, o raio da base e a altura do cilindro.

Sabendo que a medida da altura desse cilindro é o dobro da medida do raio da sua base, a área lateral desse cilindro é

1. 36π cm².
2. 27π cm².
3. 32π cm².
4. 40π cm².
5. 42π cm².

03. (EEAR) Um cilindro equilátero tem 196 π cm² de área lateral. O raio da base desse cilindro mede _______ cm.

1. 5
2. 6
3. 7
4. 8

04. (PUC-SP) O volume de um cilindro de 8 cm de altura equivale a 75% do volume de uma esfera com 8 cm de diâmetro. A área lateral do cilindro, em cm² , é

1. 42 √2π
2. 36 √3π
3. 32√2π
4. 24√3π

05. (FAMERP) A área total de um cilindro circular reto é numericamente igual ao seu volume.

Se as medidas do raio da base e da altura desse cilindro são, em uma mesma unidade de medida, r e h, respectivamente, então r é igual a:

1. h/h-1
2. 2h/2-h
3. h/1-h
4. 2h/h-2
5. h²/h-2

06. (Fuvest) Considere um cilindro C de altura h > 0 e cujo raio das circunferências, do topo e da base, é r > 0; um cilindro C1 cujo raio é igual ao de C e altura igual a h/2; e um cilindro C2 com altura h e raio igual a r/2.

Sendo V, V1 e V2 os volumes e A, A1 e A2 as áreas laterais dos cilindros C, C1 e C2, respectivamente, é correto afirmar:

1. V = V1 + V2 e A = A1 + A2
2. V = V1 + V2 e A = A1 + 2A2
3. V = V1 + 2V2 e A = A1 + 2A2
4. V = V1 + 2V2 e A = A1 + A2
5. V = 2V1 + 2V2 e A = 2A1 + 2A2

07. (UESB) As tendas de circo geralmente são montadas com o formato de um cone circular reto sobre um cilindro circular reto de mesmo raio, para criar um ambiente envolvente e atrativo. Suponha uma tenda produzida com lona que tenha um raio da base de 15 metros, com a altura da parte cilíndrica de 20 metros e da parte cônica de 8 metros.

Considerando essas informações e, também, que não foi utilizada lona no piso do circo, pode-se afirmar que a quantidade de lona (área) utilizada na produção dessa tenda foi, em m², de:

1. 855π.
2. 750π.
3. 550π.
4. 800π.
5. 450π.

08. (UEMG) Considere um cilindro equilátero reto, cujo volume é 686 π cm³, Qual a área total desse cilindro?

1. 196π cm²
2. 245π cm²
3. 294π cm²
4. 392π cm²

09. (UNEB) A diferença entre a área da base e a área lateral de um cilindro circular reto de raio r e altura 9 cm é igual ao triplo da área de um círculo de raio 9 cm.

Nessas condições, o raio do cilindro mede

1. 36 cm.
2. 27 cm.
3. 24 cm.
4. 18 cm.
5. 12 cm.

10. (Escola Naval) Um fabricante de bolas de tênis (bolas em formatos esféricos) deseja vender as bolas em embalagens cilíndricas (cilindros circulares retos) de raio R e altura H, cada uma. Em cada embalagem há n bolas de tênis de raio R, cada bola.

O fabricante deseja que a área total das superfícies das bolas seja igual à área lateral da embalagem (cilindro). Dessa forma, é correto afirmar que:

1. R = H/n.
2. R = H/2n.
3. R = H/3n.
4. R = 2H/3n.
5. R = 3H/4n.