Álgebra Linear

01. (ESA) Seja A uma matriz de ordem 3 tal que Det (A)= 4.

Então Det (2A) vale:

1. 128.
2. 64.
3. 8.
4. 32.
5. 16.

02. (EsPCEx) Para que o sistema linear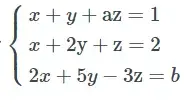 em que a e b são reais, seja possível e indeterminado, o valor de a + b é igual a

1. 10
2. 11
3. 12
4. 13
5. 14

03. (EsPCEx) Seja x um número real, I a matriz identidade de ordem 2 e A a matriz quadrada de ordem 2, cujos elementos são definidos por aij = i - j. Sobre a equação em x definida por det(A - xI) = x + det A é correto afirmar que

1. as raízes são 0 e 1/2.
2. todo x real satisfaz a equação.
3. apresenta apenas raízes inteiras.
4. uma raiz é nula e a outra negativa.
5. apresenta apenas raízes negativas.

04. (ESA) Três amigos, Abel, Bruno e Carlos, juntos possuem um total de 555 figurinhas. Sabe-se que Abel possui o triplo de Bruno menos 25 figurinhas, e que Bruno possui o dobro de Carlos mais 10 figurinhas.

Desses amigos, o que possui mais tem

1. 250 figurinhas.
2. 365 figurinhas.
3. 275 figurinhas.
4. 325 figurinhas.
5. 300 figurinhas

05. (EPCAR) Três pessoas, X, Y e Z tinham a mesma quantia em reais. X, de início, gastou 99 reais. Y deu uma parte de sua quantia para Z, e o dobro dessa parte, para X. Com essas novas quantias em reais, as três pessoas saíram para as compras e X gastou o quadrado da diferença entre 4 reais e o que Y havia dado para Z. Y e Z gastaram, cada uma, a diferença entre o quadrado doque Y havia dado a Z e 4 reais. Após esses gastos, a soma das quantias de X e Z era igual ao dobro da de Y.

É correto afirmar que X gastou no total, em reais,

1. 90
2. 99
3. 108
4. 118

06. (ESA) Dadas as matrizes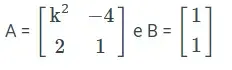

Considerando que a equação A.X = B tem solução única, podemos afirmar que

1. k = ±4
2. k = ±1
3. k ≠ ±2
4. k = ±2
5. k ≠ ±4

07. (AFA) Pedro e Maria com seus filhos Gabriel e João foram a uma clínica médica para uma revisão de saúde. Fazia parte da avaliação aferir o peso de cada um. A balança da clínica era muito antiga e tinha um defeito, só indicava pesos maiores que 60 kg

Para resolver a pesagem, procedeu-se da seguinte maneira:

Pesou-se

• Pedro, Maria e Gabriel, totalizando 150 kg

• Pedro, Gabriel e João, totalizando 117 kg

• Maria, Gabriel e João, totalizando 97 kg

• Pedro, Maria, Gabriel e João, totalizando 172 kg

Com base nessas informações, é correto afirmar que

1. com essa balança é possível pesar Gabriel e João juntos.
2. a diferença entre os pesos de Pedro e Maria é o peso de João.
3. Pedro é mais pesado que Maria e João juntos.
4. não é possível pesar Maria sozinha nessa balança.

08. (EsPCEx) No Brasil, três turistas trocaram por reais, no mesmo dia e pelas mesmas cotações, as quantias que possuíam em dólares, libras e euros, da seguinte forma:

Turista A: 10 dólares, 20 libras e 15 euros por 122 reais;

Turista B: 15 dólares, 10 libras e 20 euros por 114 reais;

Turista C: 20 dólares, 10 libras e 10 euros por 108 reais.

O valor em reais recebido por uma libra foi

1. 2,60
2. 2,80
3. 3,00
4. 3,20
5. 3,40

09. (ESA) Sabendo-se que uma matriz quadrada é invertível se, e somente se, seu determinante é não-nulo e que, se A e B são duas matrizes quadradas de mesma ordem, então det (A.B) = (det A).(det B), pode-se concluir que, sob essas condições

1. se A é invertível, então A.B é invertível.
2. se B não é invertível, então A é invertível.
3. se A.B é invertível, então A é invertível e B não é invertível.
4. se A.B não é invertível, então A ou B não é invertível.
5. se A.B é invertível, então B é invertível e A não é invertível

10. (EsPCEx) Uma tropa realizou um exercício em que soldados, sargentos e oficiais executaram módulos padronizados de tiro, consumindo, individualmente, o número de munição estabelecido conforme o seu nível hierárquico. No primeiro dia atiraram 16 soldados, 8 sargentos e 4 oficiais, totalizando 96 munições; no segundo dia, 5 soldados, 4 sargentos e 3 oficiais, totalizando 38 munições; no terceiro dia, 16 soldados, 4 sargentos e 1 oficial, totalizando 78 munições. Quantas munições foram usadas no quarto dia, quando atiraram 14 soldados, 8 sargentos e 2 oficiais?

1. 78.
2. 80.
3. 82.
4. 84.
5. 86.

11. (AFA) Considere as matrizes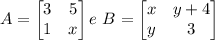

Se x e y são valores para os quais B é a transposta da Inversa da matriz A, então o valor de x+y é

1. -1
2. -2
3. -3
4. -4
5. -5

12. (ESA) Um pelotão está formado de tal maneira que todas as n filas têm n soldados. Trezentos soldados se juntam a esse pelotão e a nova formação tem o dobro de filas, cada uma, porém, com 10 soldados a menos.

Quantas filas há na nova formação?

1. 20
2. 30
3. 40
4. 60
5. 80

13. (EPCAR) Carlos, Paulo e José resolveram fazer um lanche na praça de alimentação de um shopping center.

Ao observarem o cardápio disponível, perceberam que teriam que pedir o que era denominado de “Combo”, ou seja, um combinado de vários itens por um preço já especificado.

Assim, os Combos solicitados foram:

*Combo 1 = R$15,00 : 2 hambúrgueres,1 suco e 1 sobremesa

*Combo 2 = R$ 24,00 : 4 hambúrgueres e 3 sucos

*Combo 3 = R$35,00 : 5 sucos e 3 sobremesas

O valor individual dos hambúrgueres é o mesmo, bem como o valor individual dos sucos e o valor individual das sobremesas, não importando qual Combo foi escolhido.

O quadro a seguir mostra a quantidade de cada um dos itens dos Combos que Carlos, Paulo e José consumiram:

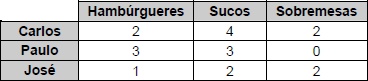
Se Carlos, Paulo e José se organizaram para descobrir o valor individual de cada item e pagaram individualmente apenas pelo que cada um consumiu, então é correto afirmar que

1. Carlos pagou R$ 9,00 a mais que Paulo.
2. a diferença entre o que Carlos e José pagaram foi de R$ 3,00
3. Paulo e José pagaram o mesmo valor.
4. Carlos pagou mais que José, que pagou mais que Paulo.

14. (EsPCEx) O Conjunto solução do sistema 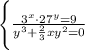é formado por dois pontos, cuja localização no plano cartesiano é

1. Ambos no primeiro quadrante.
2. Um no quarto quadrante e o outro no eixo X.
3. Um no segundo quadrante e o outro no terceiro quadrante.
4. Um no terceiro quadrante e o outro no eixo Y.
5. Um no segundo quadrante e o outro no eixo X.

15. (EsPCEx) Uma determinada empresa de biscoitos realizou uma pesquisa sobre a preferência de seus consumidores em relação a seus três produtos: biscoitos cream cracker, wafer e recheados. Os resultados indicaram que:

- 65 pessoas compram cream crackers.

- 85 pessoas compram wafers.

- 170 pessoas compram biscoitos recheados.

- 20 pessoas compram wafers, cream crackers e recheados.

- 50 pessoas compram cream crackers e recheados.

- 30 pessoas compram cream crackers e wafers.

- 60 pessoas compram wafers e recheados.

- 50 pessoas não compram biscoitos dessa empresa.

Determine quantas pessoas responderam essa pesquisa.

1. 200
2. 250
3. 320
4. 370
5. 530

16. (AFA) Sobre o polinômio A(x) , expresso pelo determinante da matriz 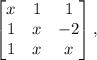,é INCORRETO afirmar que

1. não possui raízes comuns com B(x) = x² - 1
2. não possui raízes imaginárias.
3. a soma de suas raízes é igual a uma de suas raízes.
4. é divisível por P(x) = x + 2

17. (EPCAR) Na festa junina do Bairro Jardim foi montada uma barraca que vende pastéis e suco. Sabe-se que cada pastel teve um custo de R$ 0,50 e o suco já preparado para o consumo foi comprado em garrafas de 600 ml por R$ 1,20 cada. O proprietário resolveu vender o suco em copos de 250 ml ao preço de 2 reais cada copo e um pastel era oferecido em cortesia para cada copo de suco consumido. Ao afinal da festa, foram consumidas nessa barraca todas as 100 garrafas de suco que o proprietário havia adquirido e todos os clientes aceitaram a cortesia e não sobrou nenhum pastel.

É correto afirmar que, se não houve outras despesas, e o proprietário dessa barraca teve um lucro x relativo somente à venda dos sucos com suas cortesias, então a soma dos algarismos de x é igual a

1. 3
2. 6
3. 9
4. 13

18. (EsPCEx) O elemento da segunda linha e terceira coluna da matriz inversa da matriz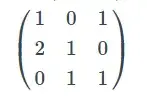

1. $\frac{2}{3}$
2. $\frac{3}{2}$
3. 0
4. -2
5. -$\frac{1}{3}$

19. (AFA) Três amigos Samuel, Vitória e Júlia, foram a uma lanchonete.

• Samuel tomou 1 guaraná, comeu 2 esfirras e pagou 5 reais.

• Vitória tomou 2 guaranás, comeu 1 esfirra e pagou 4 reais.

• Júlia tomou 2 guaranás, comeu 2 esfirras e pagou k reais.

Considerando-se que cada um dos três pagou o valor exato do que consumiu, é correto afirmar que

1. o guaraná custou o dobro da esfirra.
2. os três amigos, juntos, consumiram 16 reais.
3. cada esfirra custou 2 reais.
4. Júlia pagou 8 reais pelo que consumiu.

20. (EsPCEx) Para que o sistema linear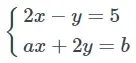 seja possível e indeterminado, o valor de a + b é:

1. –1
2. 4
3. 9
4. 14
5. 19