Geometria Plana
Lista de 19 exercícios de Matemática com gabarito sobre o tema Geometria Plana com questões da Fuvest.
01. (Fuvest 2018) Prolongando se os lados de um octógono convexo ABCDEFGH, obtém se um polígono estrelado, conforme a figura.

A soma α1 + ... + α8 vale
- 1800°
- 3600°
- 5400°
- 7200°
- 9000°
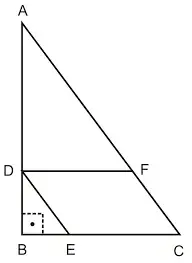
02. (Fuvest 2017) Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado BC e N o ponto médio do lado CD. Os segmentos AM e AC interceptam o segmento BN nos pontos E e F, respectivamente.
A área do triângulo AEF é igual a
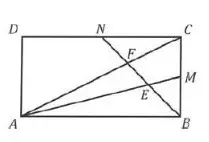
03. (Fuvest 2017) O retângulo ABCD, representado na figura, tem lados de comprimento AB = 3 e BC = 4. O ponto P pertence ao lado BC e BP = 1. Os pontos R, S e T pertencem aos lados AB, CD e AD, respectivamente. O segmento RS é paralelo a AD e intercepta DP no ponto Q. O segmento TQ é paralelo a AB.
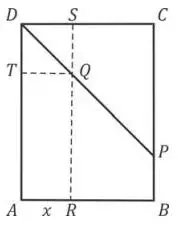
Sendo x o comprimento de AR, o maior valor da soma das áreas do retângulo ARQT, do triângulo CQP e do triângulo DQS, para x variando no intervalo aberto ]0,3[, é
04. (Fuvest 2016) Quando a Lua está em quarto crescente ou quarto minguante, o triângulo formado pela Terra, pelo Sol e pela Lua é retângulo, com a Lua no vértice do ângulo reto. O astrônomo grego Aristarco, do século III a.C., usou este fato para obter um valor
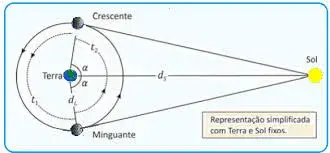
aproximado da razão entre as distâncias da Terra à Lua, dL, e da Terra ao Sol, dS.
É possível estimar a medida do ângulo α, relativo ao vértice da Terra, nessas duas fases, a partir da observação de que o tempo t1, decorrido de uma lua quarto crescente a uma lua quarto minguante, é um pouco maior do que o tempo t2, decorrido de uma lua quarto minguante a uma lua quarto crescente. Supondo que a Lua descreva em torno da Terra um movimento circular uniforme, tomando t1 = 14,9 dias e t2 = 14,8 dias, conclui-se que a razão dL/dS seria aproximadamente dada por
- cos 77,7º
- cos 80,7º
- cos 83,7º
- cos 86,7º
- cos 98,7º
05. (Fuvest 2016) No quadrilátero plano ABCD, os ângulos ABC e ADC são retos, AB = AD = 1, BC = CD = 2 e BD é uma diagonal. O cosseno do ângulo BCD vale
06. (Fuvest 2015) Os pontos A, B e C são colineares, AB = 5, BC = 2 e B está entre A e C. Os pontos C e D pertencem a uma circunferência com centro em A. Traça-se uma reta r perpendicular BD ao segmento passando pelo seu ponto médio. Chama-se de P a interseção de r com AD Então, AP + BP vale
- 4
- 5
- 6
- 7
- 8
07. (Fuvest 2015) Diz-se que dois pontos da superfície terrestre são antípodas quando o segmento de reta que os une passa pelo centro da Terra.
Podem ser encontradas, em sites da lnternet, representações, como a reproduzida abaixo, em que as áreas escuras identificam os pontos da superfície terrestre que ficam, assim como os seus antípodas, sobre terra firme. Por exemplo, os pontos antípodas de parte do sul da América do Sul estão no leste da Ásia.
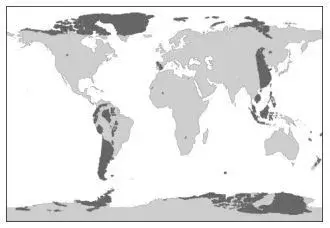
Se um ponto tem latitude x graus norte e longitude y graus leste, então seu antípoda tem latitude e longitude, respectivamente,
- x graus sul e y graus oeste.
- x graus sul e (180 – y) graus oeste.
- (90 – x) graus sul e y graus oeste.
- (90 – x) graus sul e (180 – y) graus oeste.4
- (90 – x) graus sul e (90 – y) graus oeste.
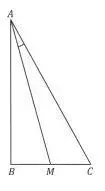
08. (Fuvest 2015) No triângulo retângulo ABC, ilustrado na figura, a hipotenusa AC mede 12 cm e o cateto BC mede 6 cm. Se M é o ponto médio de BC, então a tangente do ângulo MAC é igual a
09. (Fuvest 2014) Uma das piscinas do Centro de Práticas Esportivas da USP tem o formato de três hexágonos regulares congruentes, justapostos, de modo que cada par de hexágonos tem um lado em comum, conforme representado na figura abaixo. A distância entre lados paralelos de cada hexágono é de 25 metros.
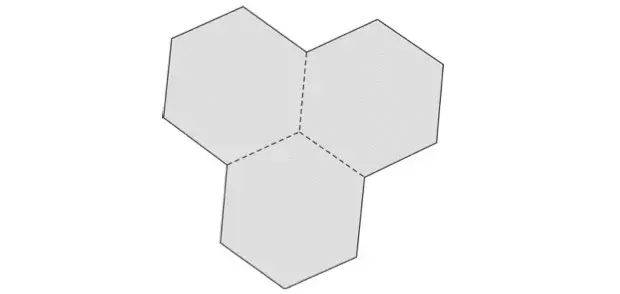
Assinale a alternativa que mais se aproxima da área da piscina.
- 1.600m²
- 1.800m²
- 2.000m²
- 2.200m²
- 2.400m²
10. (Fuvest 2014) Uma circunferência de raio está inscrita no triângulo isósceles ABC, no qual AB = AC. A altura relativa ao lado BC mede 8 cm.
O comprimento BC é, portanto, igual a
- 24 cm.
- 13 cm.
- 12 cm.
- 9 cm.
- 7 cm.
11. (Fuvest 2013) Um caminhão sobe uma ladeira com inclinação de 15º.
A diferença entre a altura final e a altura inicial de um ponto determinado do caminhão, depois de percorridos 100 m da ladeira, será de, aproximadamente,
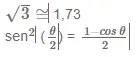
- 7 m
- 26 m
- 40 m
- 52 m
- 67 m
12. (Fuvest 2013) O mapa de uma região utiliza a escala de 1: 200 000. A porção desse mapa, contendo uma Área de Preservação Permanente (APP), está representada na figura, na qual AF e DF são segmentos de reta, o ponto G está no segmento AF, o ponto E está no segmento DF, ABEG é um retângulo e BCDE é um trapézio.
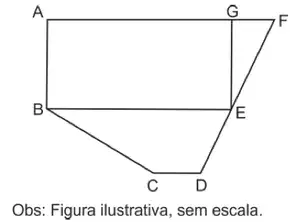
Se AF = 15, AG = 12, AB= 6, CD = 3 e = 5√5 indicam valores em centímetros no mapa real, então a área da APP é
- 100 km².
- 108 km².
- 210 km².
- 240 km².
- 444 km².
13. (Fuvest 2012) Na figura, tem-se AE paralelo a CD, BC paralelo a DE e AE = 2, α =4 5° e β = 75°. Nessas condições, a distância do ponto E ao segmento AB é igual a
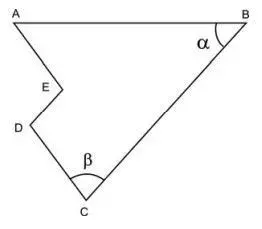
- √3
- √2
14. (Fuvest 2012) O segmento AB é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de AB de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento AB é igual a:
- √2
- 2√2
- 3√2
- √3
- 2√3
15. (Fuvest 2011) Na figura, o triângulo ABC é equilátero de lado 1, e ACDE, AFGB e BHIC são quadrados. A área do polígono DEFGHI vale
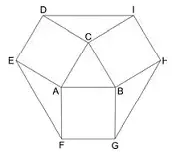
- 1+ √3
- 2 + √3
- 3 + √3
- 3 + 2√3
- 3 + 3√3
16. (Fuvest 2011) No losango ABCD de lado 1, representado na figura, tem-se que M é o ponto médio de AB, N é o ponto médio de BC e MN = √14/4 . Então, DM é igual a
o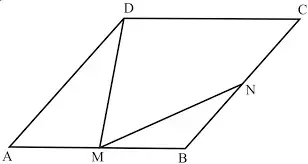
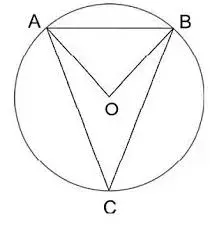
17. (Fuvest 2010) Na figura, os pontos A, B, C pertencem à circunferência de centro O e BC = a. A reta OC é perpendicular ao segmento AB e o ângulo AÔB mede π/3 radianos. Então, a área do triângulo ABC vale
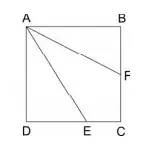
18. (Fuvest 2010) A figura representa um quadrado ABCD de lado 1. O ponto F está em BC, BF mede √5/4, o ponto E está em CD e AF é bissetriz do ângulo BÂE. Nessas condições, o segmento DE mede
19. (Fuvest 2010) Na figura, o triângulo ABC é retângulo com catetos BC = 3 e AB = 4. Além disso, o ponto D pertence ao cateto AB, o ponto E pertence ao cateto BC e o ponto F pertence à hipotenusa AC, de tal forma que DECF seja um paralelogramo. Se DE = 3/2, então a área do paralelogramo DECF vale