Geometria Plana

01. (Enem 2022) Uma pessoa precisa se deslocar de automóvel do ponto P para o ponto Q, indicados na figura, na qual as linhas verticais e horizontais simbolizam ruas.

Por causa do sentido de tráfego nessas ruas, o caminho poligonal destacado é a possibilidade mais curta de efetuar esse deslocamento. Para descrevê-lo, deve-se especificar qual o sentido a ser tomado em cada cruzamento de ruas, em relação à direção de deslocamento do automóvel, que se movimentará continuamente. Para isso, empregam-se as letras E, F e D para indicar “vire à esquerda”, “siga em frente” e “vire à direita”, respectivamente.

A sequência de letras que descreve 0 caminho poligonal destacado é

1. DDEFDDEEFFD
2. DFEFDDDEFFD
3. DFEFDDEEFFD
4. EFDFEEDDFFE
5. EFDFEEEDFFE

00. (ENEM PPL 2022) Um carcinicultor tem um viveiro de camarão cuja cerca na superfície tem formato de um trapézio isósceles. A base maior e a altura desse trapézio têm medidas, respectivamente, de 45 e 20 metros. Para manter uma produção de qualidade, ele segue o padrão de 10 camarões para cada metro quadrado da área delimitada para o viveiro, com uma produção atual correspondente a 6 000 camarões. Mantendo o mesmo padrão de qualidade, ele pretende aumentar a capacidade produtiva desse viveiro em 2 400 unidades de camarão, com a ampliação da área delimitada para o viveiro, modificando apenas a medida da base menor do trapézio.

Em quantos metros ele deverá aumentar a medida da base menor do trapézio para alcançar a capacidade produtiva desejada?

1. 21
2. 24
3. 36
4. 39
5. 54

00. (ENEM PPL 2022) Um proprietário precisa comprar tubos para ligações hidráulicas durante a reforma de sua casa, optando pela compra do material de menor custo. O engenheiro responsável pela obra afirmou ao proprietário que os tubos precisam suportar uma vazão de 1,2 litro por segundo. Para manter o padrão das tubulações já existentes na casa, os tubos devem ter 15, 20 ou 25 mm de diâmetro. Uma loja de materiais de construção apresentou ao proprietário o quadro no qual se encontram cinco tipos de tubo, com indicação de diâmetro, vazão e custo para cada um deles.

O proprietário deverá comprar

1. PVC soldável com 20 mm de diâmetro.
2. PEX com 20 mm de diâmetro.
3. Polipropileno com 15 mm de diâmetro.
4. PVC roscável com 25 mm de diâmetro.
5. Polietileno reticulado com 20 mm de diâmetro.

C

00. (ENEM PPL 2021) Um brinquedo muito comum em parques de diversões é o balanço. O assento de um balanço fica a uma altura de meio metro do chão, quando não está em uso. Cada uma das correntes que o sustenta tem medida do comprimento, em metro, indicada por x. A estrutura do balanço é feita com barras de ferro, nas dimensões, em metro, conforme a figura.

Nessas condições, o valor, em metro, de x é igual a

1. √ - 0,5
2. 1,5
3. √8 - 0,5
4. √10 - 0,5
5. √8

00. (ENEM 2022) Uma empresa de engenharia projetou uma casa com a forma de um retângulo para um de seus clientes. Esse cliente solicitou a inclusão de uma varanda em forma de L. A figura apresenta a planta baixa desenhada pela empresa, já com a varanda incluída, cujas medidas, indicadas em centímetro, representam os valores das dimensões da varanda na escala de 1 : 50.

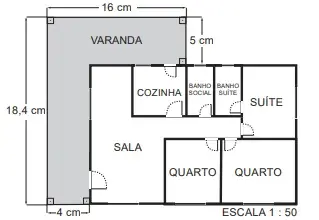
A medida real da área da varanda, em metro quadrado, é

1. 33,40.
2. 66,80.
3. 89,24.
4. 133,60.
5. 534,40.

00. (ENEM 2022) Um parque tem dois circuitos de tamanhos diferentes para corridas. Um corredor treina nesse parque e, no primeiro dia, inicia seu treino percorrendo 3 voltas em torno do circuito maior e 2 voltas em torno do menor, perfazendo um total de 1 800 m. Em seguida, dando continuidade a seu treino, corre mais 2 voltas em torno do circuito maior e 1 volta em torno do menor, percorrendo mais 1 100 m.

No segundo dia, ele pretende percorrer 5 000 m nos circuitos do parque, fazendo um número inteiro de voltas em torno deles e de modo que o número de voltas seja o maior possível.

A soma do número de voltas em torno dos dois circuitos, no segundo dia, será

1. 10.
2. 13.
3. 14.
4. 15.
5. 16.

00. (ENEM 2022) O governo de um estado pretende realizar uma obra de infraestrutura para auxiliar na integração e no processo de escoamento da produção agrícola de duas cidades. O projeto consiste na interligação direta das cidades A e B com a Rodovia 003, pela construção das Rodovias 001 e 002. As duas rodovias serão construídas em linha reta e deverão se conectar à Rodovia 003 em um mesmo ponto, conforme esboço apresentado na figura, na qual estão também indicadas as posições das cidades A e B, considerando o eixo x posicionado sobre a Rodovia 003, e cinco localizações sugeridas para o ponto de conexão entre as três rodovias.

Pretende-se que a distância percorrida entre as duas cidades, pelas Rodovias 001 e 002, passando pelo ponto de conexão, seja a menor possível.

Dadas as exigências do projeto, qual das localizações sugeridas deve ser à escolhida para o ponto de conexão?

1. I
2. II
3. III
4. IV
5. V

00. (ENEM 2022) Em uma sala de cinema, para garantir que os espectadores vejam toda a imagem projetada na tela, a disposição das poltronas deve obedecer à norma técnica da Associação Brasileira de Normas Técnicas (ABNT), que faz as seguintes indicações:

• Distância mínima (Dmin) entre a tela de projeção e o encosto da poltrona da primeira fileira deve ser de, pelo menos, 60% da largura (L) da tela.

• Distância máxima (Dmax) entre a tela de projeção e o encosto da poltrona da última fileira deve ser o dobro da largura (L) da tela, sendo aceitável uma distância de até 2,9 vezes a largura (L) da tela. Para o espaçamento entre as fileiras de poltronas, é considerada a distância de 1 metro entre os encostos de poltronas em duas fileiras consecutivas.

Disponível em: ctav.gov.br. Acesso em: 14 nov. 2013.

Uma sala de cinema, cuja largura da tela mede 12 m, está montada em conformidade com as normas da ABNT e tem suas dimensões especificadas na figura.

Pretende-se ampliar essa sala, mantendo-se na mesma posição a tela e todas as poltronas já instaladas, ampliando-se ao máximo a sala para os fundos (área de instalação de novas poltronas), respeitando-se o limite aceitável da norma da ABNT. A intenção é aumentar, ao máximo, a quantidade de poltronas da sala, instalando-se novas unidades, iguais às já instaladas.

Quantas fileiras de poltronas a sala comportará após essa ampliação?

1. 26
2. 27
3. 28
4. 29
5. 35

00. (ENEM PPL 2022) Um cliente vai a uma loja de materiais de revestimento cerâmico para adquirir porcelanato para a substituição do piso de uma sala com formato retangular, com área total de 36 m2. O vendedor dessa loja lhe oferece dois projetos.

• Projeto A: porcelanato quadrado, com 0,60 m de lado, para ser disposto de maneira que a diagonal do quadrado seja paralela ao contorno da sala. Custo da caixa com 10 peças: R$ 60,00.

• Projeto B: porcelanato quadrado, com 0,40 m de lado, para ser disposto de maneira que os lados do quadrado sejam paralelos ao contorno da sala. Custo da caixa com 12 peças: R$ 40,00.

O vendedor informa que a fábrica recomenda a compra de uma quantidade adicional do número de peças para eventual necessidade de cortes e para reserva. No caso do projeto A, devem ser adquiridos 25% a mais, e no caso do projeto B, uma quantidade 10% maior do que o valor exato da área de recobrimento.

O cliente decide, então, que irá adotar o projeto de menor custo.

O custo mínimo que o cliente deverá ter, em conformidade com seu objetivo e com as informações apresentadas, será de

1. R$ 600,00.
2. R$ 660,00.
3. R$ 720,00.
4. R$ 780,00.
5. R$ 840,00.

00. (ENEM PPL 2022) Para tornar uma pista de automobilismo mais segura, foram solicitadas intervenções em seu traçado. Os engenheiros contratados elaboraram um projeto com cinco possíveis modificações, destacadas nos setores (I), (II), (III), (IV) e (V) pelas linhas tracejadas, como mostra a figura. No entanto, na temporada atual, só é permitido que se façam duas dessas alterações.

Todos os trechos passíveis de modificação, tanto no traçado original quanto no novo traçado, são semicircunferências ou segmentos de reta.

Pretende-se que a nova pista tenha extensão mais próxima que a da original após duas modificações. Os trechos em comum da pista original e da nova pista não serão alterados.

Utilize 3 como aproximação para π.

Para atender às condições apresentadas, quais setores deverão ser modificados?

1. I e V
2. II e III
3. II e V
4. III e IV
5. IV e V

00. (ENEM PPL 2022) Um túnel viário de uma única via possui a entrada na forma de um triângulo equilátero de lado 6 m. O motorista de um caminhão com 3 m de largura deve decidir se passa por esse túnel ou se toma um caminho mais longo. Para decidir, o motorista calcula a altura que esse caminhão deveria ter para tangenciar a entrada do túnel. Considere o caminhão como um paralelepípedo reto.

Essa altura, em metro, é

1. 3
2. 3√2
3. 3√3
4. 3√2/2
5. 3√3/2

00. (ENEM PPL 2022) Uma empresa de publicidade está criando um logotipo que tem o formato indicado na figura. O círculo menor está inscrito no quadrado ABCD, e o círculo maior circunscreve o mesmo quadrado. Considere S1 a área do círculo menor e S2 a área do círculo maior

A razão da área do círculo maior para o círculo menor é igual a

1. √2
2. 1/2
3. 2
4. 8
5. 16

00. (ENEM PPL 2022) Um cortador de grama elétrico tem o cabo plugado em uma tomada fixa rente ao solo plano de um gramado. O cabo de energia mede 5 metros, e o cortador tem uma lâmina que corta 1 metro de largura. Atualmente ele corta, portanto, uma região no formato de círculo de raio 6 m, como ilustra a figura. Pretende-se usar adicionalmente um cabo extensor, de modo que seja possível cortar uma região com o dobro da área que corta atualmente.

Qual a medida aproximada, em metro, do comprimento do cabo extensor?

1. 12,0
2. 8,5
3. 6,0
4. 3,0
5. 2,5

00. (ENEM 2021) O Atomium, representado na imagem, é um dos principais pontos turísticos de Bruxelas. Ele foi construído em 1958 para a primeira grande exposição mundial depois da Segunda Guerra Mundial, a Feira Mundial de Bruxelas.

Trata-se de uma estrutura metálica construída no formato de um cubo. Essa estrutura está apoiada por um dos vértices sobre uma base paralela ao plano do solo, e a diagonal do cubo, contendo esse vértice, é ortogonal ao plano da base. Centradas nos vértices desse cubo, foram construídas oito esferas metálicas, e uma outra esfera foi construída centrada no ponto de interseção das diagonais do cubo. As oito esferas sobre os vértices são interligadas segundo suas arestas, e a esfera central se conecta a elas pelas diagonais do cubo.

Todas essas interligações são feitas por tubos cilindricos que possuem escadas em seu interior, permitindo o deslocamento de pessoas pela parte interna da estrutura. Na diagonal ortogonal à base, o deslocamento é feito por um elevador, que permite o deslocamento entre as esferas da base e a esfera do ponto mais alto, passando pela esfera central.

Considere um visitante que se deslocou pelo interior do Atomium sempre em linha reta e seguindo o menor trajeto entre dois vértices, passando por todas as arestas e todas as diagonais do cubo.

A projeção ortogonal sobre o plano do solo do trajeto percorrido por esse visitante é representada por

00. (ENEM 2021) O projeto de um contêiner, em forma de paralelepípedo reto retangular, previa a pintura dos dois lados (interno e externo) de cada uma das quatro paredes com tinta acrílica e a pintura do piso interno com tinta epóxi. O construtor havia pedido, a cinco fornecedores diferentes, orçamentos das tintas necessárias, mas, antes de iniciar a obra, resolveu mudar o projeto original, alterando o comprimento e a largura para o dobro do originalmente previsto, mantendo inalterada a altura. Ao pedir novos orçamentos aos fornecedores, para as novas dimensões, cada um deu uma resposta diferente sobre as novas quantidades de tinta necessárias.

Em relação ao previsto para O projeto original, as novas quantidades de tinta necessárias informadas pelos fornecedores foram as seguintes:

• Fornecedor I: “O dobro, tanto para as paredes quanto para o piso.”

• Fornecedor II: “O dobro para as paredes e quatro vezes para o piso.”

• Fornecedor III: “Quatro vezes, tanto para as paredes quanto para o piso.”

• Fornecedor IV: “Quatro vezes para as paredes e o dobro para o piso.”

• Fornecedor V: “Oito vezes para as paredes e quatro vezes para o piso.”

Analisando as informações dos fornecedores, o construtor providenciará a quantidade adequada de material. Considere a porta de acesso do contêiner como parte de uma das paredes.

Qual dos fornecedores prestou as informações adequadas, devendo ser o escolhido pelo construtor para a aquisição do material?

1. I
2. II
3. III
4. IV
5. V

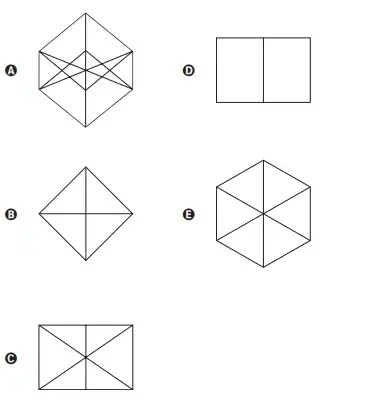
00. (ENEM 2021) Num octaedro regular, duas faces são consideradas opostas quando não têm nem arestas, nem vértices em comum. Na figura, observa-se um octaedro regular e uma de suas planificações, na qual há uma face colorida na cor cinza escuro e outras quatro faces numeradas.

Qual(is) face(s) ficará(ão) oposta(s) à face de cor cinza escuro, quando o octaedro for reconstruído a partir da planificação dada?

1. 1, 2, 3 e 4
2. 1 e 3
3. 1
4. 2
5. 4

00. (ENEM 2021) O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura

Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura. Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.

Considere 1,7 como valor aproximado para √3

Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é

1. 9,07
2. 13,60
3. 20,40
4. 27,18
5. 36,24

00. (ENEM 2021) O dono de uma loja pretende usar cartões imantados para a divulgação de sua loja. A empresa que fornecerá o serviço lhe informa que o custo de fabricação do cartão é de R$0,01 por centímetro quadrado e que disponibiliza modelos tendo como faces úteis para impressão:

• um triângulo equilátero de lado 12 cm;

• um quadrado de lado 8 cm;

• um retângulo de lados 11 cm e 8 cm;

• um hexágono regular de lado 6cm;

• um círculo de diâmetro 10 cm;

O dono da loja está disposto a pagar, no máximo, R$0,80 por cartão. Ele escolherá, dentro desse limite de preço, o modelo que tiver maior área de impressão.

Use 3 como aproximação para π e use 1,7 como aproximação para √3.

Nessas condições, o modelo que deverá ser escolhido tem como face útil para impressão um

1. triângulo.
2. quadrado.
3. retângulo.
4. hexágono.
5. círculo.

00. (ENEM PPL 2021) Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12cm.

Posteriormente, a peça triangular ABC foi dobrada, de tal maneira que o vértice B ficou sobre o segmento AC, e o segmento DE ficou paralelo ao lado AC, conforme Figura 2.

Sabe-se que, na Figura 1, o ângulo ACB é menor que o ângulo CÁB e este é menor que o ângulo ABC, e que os cortes e dobraduras foram executados corretamente pelas máquinas.

Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos DB, BE e EC?

1. 19
2. 20
3. 21
4. 24

00. (ENEM PPL 2021) Um suporte será instalado no box de um banheiro para serem colocados recipientes de xampu, condicionador e sabonete líquido, sendo que o recipiente de cada produto tem a forma de um cilindro circular reto de medida do raio igual a 3 cm. Para maior conforto no interior do box, a proprietária do apartamento decidiu comprar o suporte que tiver a base de menor área, desde que a base de cada recipiente ficasse inteiramente sobre o suporte. Nas figuras, vemos as bases desses suportes, nas quais todas as medidas indicadas estão em centímetro.

Utilize 3,14 como aproximação para 7.

Para atender à sua decisão, qual tipo de suporte a proprietária comprou?

1. I
2. II
3. III
4. IV
5. V

00. (ENEM PPL 2021) Uma empresa produz painéis solares de energia elétrica, com a forma de retângulo, que geram 5 MWh (megawatts-hora) por metro quadrado. Cada painel tem 3 m de largura e 6 m de comprimento. O selo verde de eficiência é obtido se cada painel solar gerar, no mínimo, 150 MWh de energia solar. Para obter o selo verde, a empresa decide alterar apenas a largura dos seus painéis solares.

O número mínimo, em metro, que a empresa deve aumentar na largura dos seus painéis solares é

1. 2.
2. 4.
3. 5.
4. 10.
5. 12.

1. (Enem 2020) A lei municipal para a edificação de casas em lotes de uma cidade determina que sejam obedecidos os seguintes critérios:

afastamento mínimo de 4 m da rua;

afastamento mínimo de 1 m da divisa com outro lote;

área total construída da casa entre 40% e 50% da área total do lote.

Um construtor submeteu para aprovação na prefeitura dessa cidade uma planta com propostas para a construção de casas em seus 5 lotes. Cada lote tem área medindo 200 m2.

A imagem apresenta um esquema, sem escala, no qual estão representados os lotes, as ruas e os afastamentos considerados nos projetos entre as casas e as divisas dos lotes. As medidas indicadas no esquema estão expressas em metro.

A prefeitura aprovará apenas a planta da casa

1. 1.
2. 2.
3. 3.
4. 4.
5. 5.

2. (Enem 2020) Azulejo designa peça de cerâmica vitrificada e/ou esmaltada usada, sobretudo, no revestimento de paredes. A origem das técnicas de fabricação de azulejos é oriental, mas sua expansão pela Europa traz consigo uma diversificação de estilos, padrões e usos, que podem ser decorativos, utilitários e arquitetônicos.

Disponível em: itaucultural.org.br. Acesso em: 31 jul. 2012.

Azulejos no formato de octógonos regulares serão utilizados para cobrir um painel retangular conforme ilustrado na figura.

Entre os octógonos e na borda lateral dessa área, será necessária a colocação de 15 azulejos de outros formatos para preencher os 15 espaços em branco do painel. Uma loja oferece azulejos nos seguintes formatos:

1 — Triângulo retângulo isósceles;

2 — Triângulo equilátero;

3 — Quadrado.

Os azulejos necessários para o devido preenchimento das áreas em branco desse painel são os de formato

1. 1.
2. 3.
3. 1 e 2.
4. 1 e 3.
5. 2 e 3.

3. (Enem 2020) O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se um esboço geométrico da situação. Em seguida, subdividese o espaço total em trechos, quantificando a densidade, da seguinte forma:

• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção;

• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local;

• 6 pessoas por metro quadrado, se elas estiverem paradas.

É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1.000 pessoas para cada carro de som fotografado.

Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente da principal: QR.

Obs.: a figura não está em escala (considere as medidas dadas).

Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a

1. 110.000
2. 104.000
3. 93.000
4. 92.000
5. 87.000

4. (Enem Digital 2020) Uma empresa deseja construir um edifício residencial de 12 pavimentos, num lote retangular de lados medindo 22 e 26 m. Em 3 dos lados do lote serão construídos muros. A frente do prédio será sobre o lado do lote de menor comprimento. Sabe-se que em cada pavimento 32 m²serão destinados à área comum (hall de entrada, elevadores e escada), e o restante da área será destinado às unidades habitacionais. A legislação vigente exige que prédios sejam construídos mantendo distâncias mínimas dos limites dos lotes onde se encontram. Em obediência à legislação, o prédio ficará 5 m afastado da rua onde terá sua entrada, 3 m de distância do muro no fundo do lote e 4 m de distância dos muros nas laterais do lote, como mostra a figura.

A área total, em metro quadrado, destinada às unidades habitacionais desse edifício será de

1. 2 640.
2. 3 024.
3. 3 840.
4. 6 480.
5. 6 864

5. (Enem Digital 2020) Considere o guindaste mostrado nas figuras, em duas posições (1 e 2). Na posição 1, o braço de movimentação forma um ângulo reto com o cabo de aço CB que sustenta uma esfera metálica na sua extremidade inferior.

Na posição 2, o guindaste elevou seu braço de movimentação e o novo ângulo formado entre o braço e o cabo de aço ED, que sustenta a bola metálica, é agora igual a 60°.

Assuma que os pontos A, B e C, na posição 1, formam o triângulo T₁ e que os pontos A, D e E, na posição 2, formam o triângulo T₂, os quais podem ser classificados em obtusângulo, retângulo ou acutângulo, e também em equilátero, isósceles ou escaleno.

Segundo as classificações citadas, os triângulos T₁ e T2 são identificados, respectivamente, como

1. retângulo escaleno e retângulo isósceles.
2. acutângulo escaleno e retângulo isósceles.
3. retângulo escaleno e acutângulo escaleno.
4. acutângulo escaleno e acutângulo equilátero.
5. retângulo escaleno e acutângulo equilátero.

6. (Enem Digital 2020) Um marceneiro visitou 5 madeireiras para comprar tábuas que lhe permitissem construir 5 prateleiras de formato retangular, de dimensões iguais a 30 cm de largura por 120 cm de comprimento cada, tendo como objetivo minimizar a sobra de madeira, podendo, para isso, fazer qualquer tipo de emenda. As dimensões das tábuas encontradas nas madeireiras estão descritas no quadro.

Em qual madeireira o marceneiro deve comprar as tábuas para atingir seu objetivo?

1. I
2. II
3. III
4. IV
5. V

7. (Enem Digital 2020) Os tempos gastos por três alunos para resolver um mesmo exercício de matemática foram: 3,25 minutos; 3,4 minutos e 191 segundos.

O tempo gasto a mais, em segundo, pelo aluno que concluiu por último a resolução do exercício, em relação ao primeiro que o finalizou, foi igual a

1. 13.
2. 14.
3. 15.
4. 21.
5. 29

8. (Enem PPL 2020) Os alunos do curso de matemática de uma universidade desejam fazer uma placa de formatura, no formato de um triângulo equilátero, em que os seus nomes aparecerão dentro de uma região quadrada, inscrita na placa, conforme a figura.

Considerando que a área do quadrado, em que aparecerão os nomes dos formandos, mede 1 m2 , qual é aproximadamente a medida, em metro, de cada lado do triângulo que representa a placa? (Utilize 1,7 como valor aproximado para 3 ).

1. 1,6
2. 2,1
3. 2,4
4. 3,7
5. 6,4

9. (Enem PPL 2020) Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L

A fórmula correta é

10. (Enem PPL 2020) Dois atletas partem de pontos, respectivamente P₁ e P₂ , em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é R₁ e o raio do semicírculo menor é R₂.

Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco. Nas condições apresentadas, a razão da medida do ângulo P_2CP₁ pela diferença L− I é dada por

11. (Enem PPL 2020) Foi feita uma pesquisa sobre a escolaridade dos funcionários de uma empresa. Verificou-se que 1/4 dos homens que ali trabalham têm o ensino médio completo, enquanto 2/3 das mulheres que trabalham na empresa têm o ensino médio completo. Constatou-se, também, que entre todos os que têm o ensino médio completo, metade são homens.

A fração que representa o número de funcionários homens em relação ao total de funcionários dessa empresa é

1. 1/8
2. 3/11
3. 11/24
4. 2/3
5. 8/11

12. (Enem PPL 2020) Pretende-se comprar uma mesa capaz de acomodar 6 pessoas, de modo que, assentadas em torno da mesa, cada pessoa disponha de, pelo menos, 60 cm de espaço livre na borda do tampo da mesa, que deverá ter a menor área possível. Na loja visitada há mesas com tampos nas formas e dimensões especificadas:

• Mesa I: hexágono regular, com lados medindo 60 cm;

• Mesa II: retângulo, com lados medindo 130 cm e 60 cm;

• Mesa III: retângulo, com lados medindo 120 cm e 60 cm;

• Mesa IV: quadrado, com lados medindo 60 cm;

• Mesa V: triângulo equilátero, com lados medindo 120 cm.

A mesa que atende aos critérios especificados é a

1. I.
2. II.
3. III.
4. IV.
5. V.

13. (Enem PPL 2020) Um estudante, morador da cidade de Contagem, ouviu dizer que nessa cidade existem ruas que formam um hexágono regular. Ao pesquisar em um sítio de mapas, verificou que o fato é verídico, como mostra a figura.

Ele observou que o mapa apresentado na tela do computador estava na escala 1 : 20 000. Nesse instante, mediu o comprimento de um dos segmentos que formam os lados desse hexágono, encontrando 5 cm.

Se esse estudante resolver dar uma volta completa pelas ruas que formam esse hexágono, ele percorrerá, em quilômetro,

1. 1.
2. 4.
3. 6.
4. 20.
5. 24.

14. (Enem PPL 2019) O dono de um salão de festas precisa decorar cinco pilastras verticais cilíndricas idênticas, cujo raio da base mede 10 cm. O objetivo é revestir integralmente essas pilastras com faixas de menor comprimento possível, de modo que cada uma tenha seis faixas de cor preta e cinco faixas de cor branca, conforme ilustrado na figura.

Ele orçou as faixas em cinco lojas que as comercializam na largura e nas cores desejadas, porém, em todas elas, só são vendidas peças inteiras. Os comprimentos e os respectivos preços das peças comercializadas por loja estão apresentados no quadro.

O dono do salão de festas decidiu efetuar a compra em uma única loja, optando por aquela em que a compra ficaria mais barata.

Utilize 3 como valor aproximado para π.

A loja na qual o dono do salão de festas deve comprar as peças necessárias para confeccionar as faixas é

1. I
2. II.
3. III.
4. IV.
5. V.

15. (Enem PPL 2019) A unidade de medida utilizada para anunciar o tamanho das telas de televisores no Brasil é a polegada, que corresponde a 2,54 cm. Diferentemente do que muitos imaginam, dizer que a tela de uma TV tem X polegadas significa que a diagonal do retângulo que representa sua tela mede X polegadas, conforme ilustração.

O administrador de um museu recebeu uma TV convencional de 20 polegadas, que tem como razão do comprimento (C) pela altura (A) a proporção 4 : 3, e precisa calcular o comprimento (C) dessa TV a fim de colocá-la em uma estante para exposição.

A tela dessa TV tem medida do comprimento C, em centímetro, igual a

1. 12,00.
2. 16,00.
3. 30,48.
4. 40,64.
5. 50,80.

16. (Enem PPL 2019) No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.

Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura.

A razão entre $\stackrel{-}{BC}$ e $\stackrel{-}{AD}$ que determina áreas iguais para os cinco triângulos mostrados na figura é

1. $\frac{1}{3}$
2. $\frac{2}{3}$
3. $\frac{2}{5}$
4. $\frac{3}{5}$
5. $\frac{5}{6}$