Geometria Analı́tica
Lista de 18 exercícios de Matemática com gabarito sobre o tema Geometria Analı́tica (Plano, Reta e Circunferência) com questões do Enem.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Geometria Analı́tica.
01. (Enem PPL 2021) Uma moça estacionou seu carro na interseção da Rua 1 com a Avenida A. Ela está hospedada em um hotel na Rua 3, posicionado a exatos 40 metros de distância da Avenida À, contados a partir da Avenida A em direção à Avenida B.
No mapa está representado um plano cartesiano cujo eixo das abscissas coincide com a Avenida À e o das ordenadas, com a Rua 1, sendo a origem (0, 0) o local onde se encontra estacionado o veículo. Os quarteirões formados pelos cruzamentos dessas vias formam quadrados de lados medindo 100 m.

A ordenada do ponto que representa a localização do hotel é
- -60.
- -40.
- 0.
- 40.
- 60.
02. (Enem 2021) O administrador de um teatro percebeu que, com o
ingresso do evento a R$ 20,00, um show conseguia atrair 200 pessoas e que, a cada R$ 1,00 de redução no preço do ingresso, o número de pessoas aumentava em 40. Ele sabe que os donos do teatro só admitem trabalhar com valores inteiros para os ingressos, pela dificuldade de disponibilizar troco, e pretende convencê-los a diminuir o preço do ingresso. Assim, apresentará um gráfico da arrecadação em função do valor do desconto no preço atual do ingresso.
O gráfico que mais se assemelha ao que deve ser elaborado pelo administrador é
03. (Enem PPL 2021) A escala de temperatura Delisle (CD), inventada no século XVIII pelo astrônomo francês Joseph-Nicholas Delisle, a partir da construção de um termômetro, foi utilizada na Rússia no século XIX. A relação entre as temperaturas na escala Celsius (ºC) e na escala Delisle está representada no gráfico pela reta que passa pelos pontos Ae B.

Qual é a relação algébrica entre as temperaturas nessas duas escalas?
- 2D+C=100
- 2D+3C=150
- 3D+2C=300
- 2D+3C=300
- 3D+2C=450
1. (Enem 2020) No período de fim de ano, o síndico de um condomínio resolveu colocar, em um poste, uma iluminação natalina em formato de cone, lembrando uma árvore de Natal, conforme as figuras 1 e 2.

A árvore deverá ser feita colocando-se mangueiras de iluminação, consideradas segmentos de reta de mesmo comprimento, a partir de um ponto situado a 3 m de altura no poste até um ponto de uma circunferência de fixação, no chão, de tal forma que esta fique dividida em 20 arcos iguais. O poste está fixado no ponto C (centro da circunferência) perpendicularmente ao plano do chão.
Para economizar, ele utilizará mangueiras de iluminação aproveitadas de anos anteriores, que juntas totalizaram pouco mais de 100 m de comprimento, dos quais ele decide usar exatamente 100 m e deixar o restante como reserva.
Para que ele atinja seu objetivo, o raio, em metro, da circunferência deverá ser de
- 4,00.
- 4,87.
- 5,00.
- 5,83.
- 6,26.
2. (Enem 2020) Em um jogo desenvolvido para uso no computador, objetos tridimensionais vão descendo do alto da tela até alcançarem o plano da base. O usuário pode mover ou girar cada objeto durante sua descida para posicioná-lo convenientemente no plano horizontal. Um desses objetos é formado pela justaposição de quatro cubos idênticos, formando assim um sólido rígido, como ilustrado na figura

Para facilitar a movimentação do objeto pelo usuário, o programa projeta ortogonalmente esse sólido em três planos quadriculados perpendiculares entre si, durante sua descida.
A figura que apresenta uma possível posição desse sólido, com suas respectivas projeções ortogonais sobre os três planos citados, durante sua descida é
3. (Enem PPL 2019) Na anestesia peridural, como a usada nos partos, o médico anestesista precisa introduzir uma agulha nas costas do paciente, que atravessará várias camadas de tecido até chegar a uma região estreita, chamada espaço epidural, que envolve a medula espinhal. A agulha é usada para injetar um líquido anestésico, e a força que deve ser aplicada à agulha para fazê-la avançar através dos tecidos é variável.
A figura é um gráfico do módulo F da força (em newton) em função do deslocamento x da ponta da agulha (em milímetro) durante uma anestesia peridural típica.
Considere que a velocidade de penetração da agulha deva ser a mesma durante a aplicação da anestesia e que a força aplicada à agulha pelo médico anestesista em cada ponto deve ser proporcional à resistência naquele ponto.
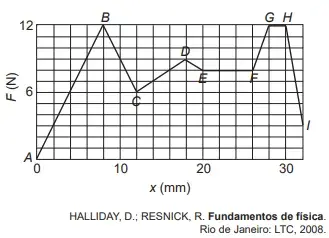
Com base nas informações apresentadas, a maior resistência à força aplicada observa-se ao longo do segmento
- AB.
- FG.
- EF.
- GH.
- HI.
4. (Enem 2019) Um grupo de países criou uma instituição responsável por organizar o Programa Internacional de Nivelamento de Estudos (PINE) com o objetivo de melhorar os índices mundiais de educação. Em sua sede foi construída uma escultura suspensa, com a logomarca oficial do programa, em três dimensões, que é formada por suas iniciais, conforme mostrada na figura.

Essa escultura está suspensa por cabos de aço, de maneira que o espaçamento entre letras adjacentes é o mesmo, todas têm igual espessura e ficam dispostas em posição ortogonal ao solo, como ilustrado a seguir

Ao meio-dia, com o sol a pino, as letras que formam essa escultura projetam ortogonalmente suas sombras sobre o solo.
A sombra projetada no solo é
5. (Enem 2018) Para criar um logotipo, um profissional da área de design gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.

Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.
Esse conjunto é dado pelos pares ordenados (x ; y) e começar estilo tamanho matemático 14px reto números naturais fim do estilo x começar estilo tamanho matemático 14px reto números naturais fim do estilo, tais que
- 0 ≤ x ≤ y ≤ 10
- 0 ≤ y ≤ x ≤ 10
- 0 ≤ x ≤ 10, 0 ≤ y ≤ 10
- 0 ≤ x + y ≤ 10
- 0 ≤ x + y ≤ 20
6. (Enem 2018) Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando “tiros”, seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0 ; 4), 6(4 ; 4), C(4 ; 0), D(2 ; 2) e E(0; 2).

Passando pelo ponto A, qual equação forneceria a maior pontuação?
- x = 0
- y = 0
- x² + y² =16
- x² + (y-2)² = 4
- (x - 2)² + (y - 2)² = 8
7. (Enem 2018) Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30 m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, da temperatura menos elevada.
Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é
- 30
- 40
- 45
- 60
- 68
8. (Enem 2018) Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30 m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, da temperatura menos elevada.
Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é
- 30
- 40
- 45
- 60
- 68
9. (Enem 2017) Um menino acaba de se mudar para um novo bairro e deseja ir à padaria. Pediu ajuda a um amigo que lhe forneceu um mapa com pontos numerados, que representam cinco locais de interesse, entre os quais está a padaria. Além disso, o amigo passou as seguintes instruções: a partir do ponto em que você se encontra, representado pela letra X, ande para oeste, vire à direita na primeira rua que encontrar, siga em frente e vire à esquerda na próxima rua. A padaria estará logo a seguir

A padaria está representada pelo ponto numerado com
- 1
- 2
- 3
- 4
- 5
10. (Enem 2017) O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade V de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a) (v + b) = K, com a, b e K constantes.
Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:
| TIPO DE CURVA |
|---|
| Semirreta oblíqua |
| Semirreta horizontal |
| Ramo de parábola |
| Arco de circunferência |
| Ramo de hipérbole |
O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p. V). Admita que K > 0.
Disponível em: http://rspb.royalsocietypublishing.org. Acesso em: 14jul2015 (adaptado).
O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo
- Semirreta oblíqua.
- semirreta horizontal.
- ramo de parábola.
- arco de circunferência.
- ramo de hipérbole.
11. (Enem 2016) Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
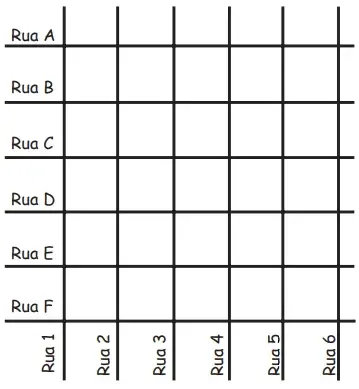
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
- 3 e C
- 4 e C
- 4 e D
- 4 e E
- 5 e C
12. (Enem PPL 2015) Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.
A seguir há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.
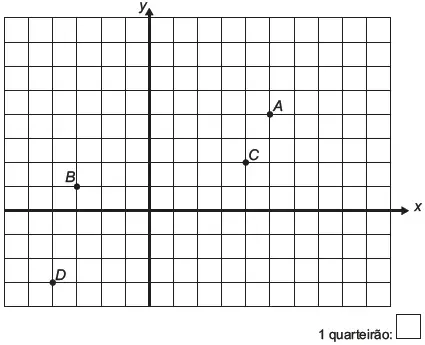
Suponha que uma rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontre num ponto cujas coordenadas satisfaçam à inequação: x² + y² – 2x – 4y – 31 ≤ 0.
A fim de avaliar a qualidade do sinal, e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio enquanto os outros não.
Os estabelecimentos que conseguem ouvir a rádio são apenas
- A e C.
- B e C.
- B e D.
- A, B e C.
- B, C e D.
13. (Enem 2016) Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.

Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
- diminuir em 2 unidades
- diminuir em 4 unidades
- aumentar em 2 unidades.
- aumentar em 4 unidades.
- aumentar em 8 unidades.
14. (Enem 2016) Uma região de uma fábrica deve ser isolada, pois nela os empregados ficam expostos a riscos de acidentes. Essa região está representada pela porção de cor cinza (quadrilátero de área S) na figura.
Para que os funcionários sejam orientados sobre a localização da área isolada, cartazes informativos serão afixados por toda fábrica. Para confeccioná-los, um programador utilizará um software que permite desenhar essa região a partir de um conjunto de desigualdades algébricas.
As desigualdades que devem ser utilizadas no referido software, para o desenho da região de isolamento, são
- 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 8; x ≤ 9
- 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 9; x ≤ 8
- 3y – x ≥ 0; 2y – x ≤ 0; y ≤ 9; x ≤ 8
- 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 8; x ≤ 9
- 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 9; x ≤ 8
15. (Enem 2015) A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.
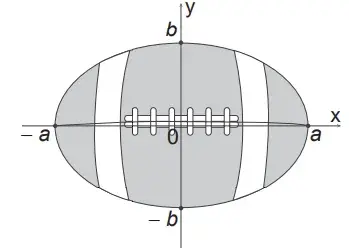
Considere que o volume aproximado dessa bola é dado por V = 4ab².
O volume dessa bola, em função apenas de b, é dado por
- 8b³
- 6b³
- 5b³
- 4b³
- 2b³
16. (Enem 2015) Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
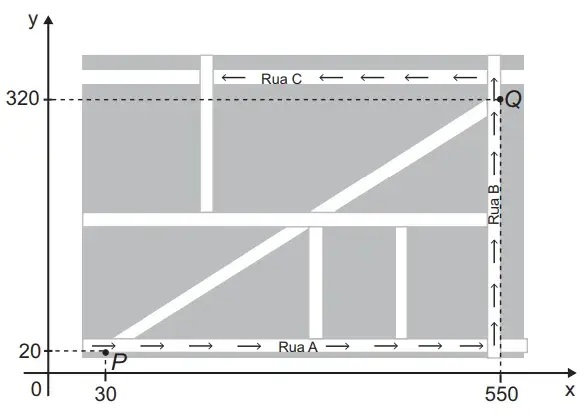
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto de parada são
- (290 ; 20).
- (410 ; 0).
- (410 ; 20).
- (440 ; 0).
- (440 ; 20).
17. (Enem 2009) Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d≤ sobre a circunferência.

Então, o ponto Q percorrerá, no eixo x, uma distância dada por
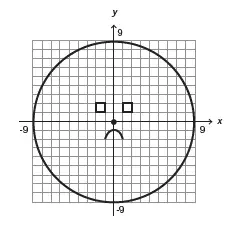
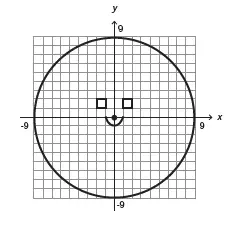
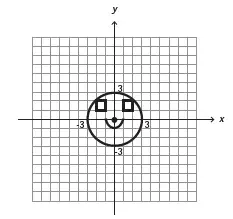
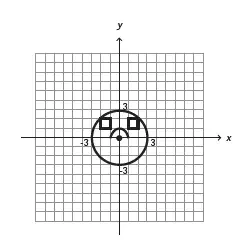
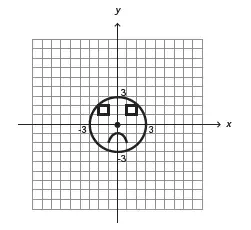
18. (Enem 2013) Durante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:
(I) é a circunferência de equação x2 + y2 = 9;
(II) é a parábola de equação y = −x2 − 1, com x variando de -1 a 1;
(III) é o quadrado formado pelos vértices (-2, 1), (-1, 1), (-1, 2) e (-2, 2);
(IV) é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
(V) é o ponto (0, 0).
A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura. Qual destas figuras foi desenhada pelo professor?