Geometria, Enem PPL 2019

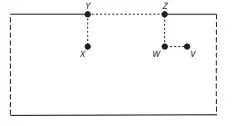
01. (Enem PPL 2019) Uma formiga encontra-se no ponto X, no lado externo de um copo que tem a forma de um cilindro reto. No lado interno, no ponto V, existe um grão de açúcar preso na parede do copo. A formiga segue o caminho XYZWV (sempre sobre a superfície lateral do copo), de tal forma que os trechos ZW e WV são realizados na superfície interna do copo. O caminho XYZWV é mostrado na figura.

Sabe-se que: os pontos X, V, W se encontram à mesma distância da borda; o trajeto WV é o mais curto possível; os trajetos XY e ZW são perpendiculares à borda do copo; e os pontos X e V se encontram diametralmente opostos.

Supondo que o copo é de material recortável, realiza-se um corte pelo segmento unindo P a Q, perpendicular à borda do copo, e recorta-se também sua base, obtendo então uma figura plana. Desconsidere a espessura do copo.

Considerando apenas a planificação da superfície lateral do copo, a trajetória da formiga é

02. (Enem PPL 2019) O dono de um salão de festas precisa decorar cinco pilastras verticais cilíndricas idênticas, cujo raio da base mede 10 cm. O objetivo é revestir integralmente essas pilastras com faixas de menor comprimento possível, de modo que cada uma tenha seis faixas de cor preta e cinco faixas de cor branca, conforme ilustrado na figura.

Ele orçou as faixas em cinco lojas que as comercializam na largura e nas cores desejadas, porém, em todas elas, só são vendidas peças inteiras. Os comprimentos e os respectivos preços das peças comercializadas por loja estão apresentados no quadro.

O dono do salão de festas decidiu efetuar a compra em uma única loja, optando por aquela em que a compra ficaria mais barata.

Utilize 3 como valor aproximado para π.

A loja na qual o dono do salão de festas deve comprar as peças necessárias para confeccionar as faixas é

1. I
2. II.
3. III.
4. IV.
5. V.

03. (Enem PPL 2019) Na anestesia peridural, como a usada nos partos, o médico anestesista precisa introduzir uma agulha nas costas do paciente, que atravessará várias camadas de tecido até chegar a uma região estreita, chamada espaço epidural, que envolve a medula espinhal. A agulha é usada para injetar um líquido anestésico, e a força que deve ser aplicada à agulha para fazê-la avançar através dos tecidos é variável.

A figura é um gráfico do módulo F da força (em newton) em função do deslocamento x da ponta da agulha (em milímetro) durante uma anestesia peridural típica.

Considere que a velocidade de penetração da agulha deva ser a mesma durante a aplicação da anestesia e que a força aplicada à agulha pelo médico anestesista em cada ponto deve ser proporcional à resistência naquele ponto.

Com base nas informações apresentadas, a maior resistência à força aplicada observa-se ao longo do segmento

1. AB.
2. FG.
3. EF.
4. GH.
5. HI.

04. (Enem PPL 2019) A unidade de medida utilizada para anunciar o tamanho das telas de televisores no Brasil é a polegada, que corresponde a 2,54 cm. Diferentemente do que muitos imaginam, dizer que a tela de uma TV tem X polegadas significa que a diagonal do retângulo que representa sua tela mede X polegadas, conforme ilustração.

O administrador de um museu recebeu uma TV convencional de 20 polegadas, que tem como razão do comprimento (C) pela altura (A) a proporção 4 : 3, e precisa calcular o comprimento (C) dessa TV a fim de colocá-la em uma estante para exposição.

A tela dessa TV tem medida do comprimento C, em centímetro, igual a

1. 12,00.
2. 16,00.
3. 30,48.
4. 40,64.
5. 50,80.

05. (Enem PPL 2019) As coordenadas usualmente utilizadas na localização de um ponto sobre a superfície terrestre são a latitude e a longitude. Para tal, considera-se que a Terra tem a forma de uma esfera.

Um meridiano é uma circunferência sobre a superfície da Terra que passa pelos polos Norte e Sul, representados na figura por PN e PS. O comprimento da semicircunferência que une os pontos PN e PS tem comprimento igual a 20 016 km. A linha do Equador também é uma circunferência sobre a superfície da Terra, com raio igual ao da Terra, sendo que o plano que a contém é perpendicular ao que contém qualquer meridiano.

Seja P um ponto na superfície da Terra, C o centro da Terra e o segmento $\stackrel{-}{PC}$ um raio, conforme mostra a figura. Seja ϕ o ângulo que o segmento $\stackrel{-}{PC}$ faz com o plano que contém a linha do Equador. A medida em graus de ϕ é a medida da latitude de P.

Suponha que a partir da linha do Equador um navio viaja subindo em direção ao Polo Norte, percorrendo um meridiano, até um ponto P com 30 graus de latitude.

Quantos quilômetros são percorridos pelo navio?

1. 1 668
2. 3 336
3. 5 004
4. 6 672
5. 10 008

06. (Enem PPL 2019) Para decorar sua casa, uma pessoa comprou um vaso de vidro em forma de um paralelepípedo retangular, cujas medidas internas são: 40 cm de comprimento, 35 cm de largura e 60 cm de altura. Em seguida, foi até uma floricultura e escolheu uma planta aquática para colocar nesse vaso. Segundo uma proposta do gerente do local, essa pessoa avaliou a possibilidade de enfeitar o vaso colocando uma certa quantidade de pedrinhas artificiais brancas, de volume igual a 100 cm³cada uma delas, que ficarão totalmente imersas na água que será colocada no vaso. O gerente alertou que seria adequado, em função da planta escolhida, que metade do volume do vaso fosse preenchido com água e que, após as pedrinhas colocadas, a altura da água deveria ficar a 10 cm do topo do vaso, dando um razoável espaço para o crescimento da planta. A pessoa aceitou as sugestões apresentadas, adquirindo, além da planta, uma quantidade mínima de pedrinhas, satisfazendo as indicações do gerente.

Nas condições apresentadas, a quantidade de pedrinhas compradas foi

1. 140.
2. 280.
3. 350.
4. 420.
5. 700.

07. (Enem PPL 2019) Uma empresa especializou-se no aluguel de contêineres que são utilizados como unidades comerciais móveis. O modelo padrão alugado pela empresa tem altura de 2,4 m e as outras duas dimensões (largura e comprimento), 3,0 m e 7,0 m, respectivamente.

Um cliente solicitou um contêiner com altura padrão, porém, com largura 40% maior e comprimento 20% menor que as correspondentes medidas do modelo padrão. Para atender às necessidades de mercado, a empresa também disponibiliza um estoque de outros modelos de contêineres, conforme o quadro

Dos modelos disponíveis, qual atende às necessidades do cliente?

1. I
2. II
3. III
4. IV
5. V

08. (Enem PPL 2019) No ano de 1751, o matemático Euler conseguiu demonstrar a famosa relação para poliedros convexos que relaciona o número de suas faces (F), arestas (A) e vértices (V): V + F = A + 2. No entanto, na busca dessa demonstração, essa relação foi sendo testada em poliedros convexos e não convexos. Observou-se que alguns poliedros não convexos satisfaziam a relação e outros não. Um exemplo de poliedro não convexo é dado na figura. Todas as faces que não podem ser vistas diretamente são retangulares.

Qual a relação entre os vértices, as faces e as arestas do poliedro apresentado na figura?

1. V + f = A
2. V + f = A - 1
3. V + f = A + 1
4. V + f = A + 2
5. V + f = A + 3

09.(Enem PPL 2019) Muitos restaurantes servem refrigerantes em copos contendo limão e gelo. Suponha um copo de formato cilíndrico, com as seguintes medidas: diâmetro = 6 cm e altura = 15 cm. Nesse copo, há três cubos de gelo, cujas arestas medem 2 cm cada, e duas rodelas cilíndricas de limão, com 4 cm de diâmetro e 0,5 cm de espessura cada. Considere que, ao colocar o refrigerante no copo, os cubos de gelo e os limões ficarão totalmente imersos. (Use 3 como aproximação para π).

O volume máximo de refrigerante, em centímetro cúbico, que cabe nesse copo contendo as rodelas de limão e os cubos de gelo com suas dimensões inalteradas, é igual a

1. 107.
2. 234.
3. 369.
4. 391.
5. 405.

10. (Enem PPL 2019) No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.

Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura.

A razão entre $\stackrel{-}{BC}$ e $\stackrel{-}{AD}$ que determina áreas iguais para os cinco triângulos mostrados na figura é

1. $\frac{1}{3}$
2. $\frac{2}{3}$
3. $\frac{2}{5}$
4. $\frac{3}{5}$
5. $\frac{5}{6}$

11. (Enem PPL 2019) O quadro apresenta a quantidade de um tipo de pão vendido em uma semana em uma padaria.

O dono da padaria decidiu que, na semana seguinte, a produção diária desse tipo de pão seria igual ao número de pães vendidos no dia da semana em que tal quantidade foi a mais próxima da média das quantidades vendidas na semana.

O dia da semana utilizado como referência para a quantidade de pães a serem produzidos diariamente foi

1. domingo.
2. segunda-feira.
3. terça-feira.
4. quarta-feira.
5. sábado.

12. (Enem PPL 2019) Uma pista circular delimitada por duas circunferências concêntricas foi construída. Na circunferência interna dessa pista, de raio 0,3 km, serão colocados aparelhos de ginástica localizados nos pontos P, Q e R, conforme a figura.

O segmento RP é um diâmetro dessa circunferência interna, e o ângulo P $\stackrel{\wedge \; <!--\; logical\; and\; -->}{R}$Q tem medida igual a $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}}{5}$ radianos.

Para uma pessoa ir do ponto P ao ponto Q andando pela circunferência interna no sentido anti-horário, ela percorrerá uma distância, em quilômetro, igual a

1. 0,009π
2. 0,03π
3. 0,06π
4. 0,12π
5. 0,18π

13. (Enem PPL 2019) Uma empresa, investindo na segurança, contrata uma firma para instalar mais uma câmera de segurança no teto de uma sala. Para iniciar o serviço, o representante da empresa informa ao instalador que nessa sala já estão instaladas duas câmeras e, a terceira, deverá ser colocada de maneira a ficar equidistante destas. Além disso, ele apresenta outras duas informações:

(I) um esboço em um sistema de coordenadas cartesianas, do teto da sala, onde estão inseridas as posições das câmeras 1 e 2, conforme a figura.

(II) cinco relações entre as coordenadas (x ; y) da posição onde a câmera 3 deverá ser instalada.

R1: y = x

R2: y = -3x + 5

R3: y = -3x + 10
R4: y = $\frac{1}{3}$ x + $\frac{5}{3}$
R5: y = $\frac{1}{3}$ x + $\frac{1}{\mathrm{10}}$

O instalador, após analisar as informações e as cinco relações, faz a opção correta dentre as relações apresentadas para instalar a terceira câmera.

A relação escolhida pelo instalador foi a

1. R1.
2. R2.
3. R3.
4. R4.
5. R5.