Home > Banco de Questões > Matemática >

Funções III

Lista de 20 exercícios de Matemática com gabarito sobre o tema Funções III com questões do Enem.


Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Funções III.




1. (Enem 2009) Uma pousada oferece pacotes promocionais para atrair casais a se hospedarem por até oito dias. A hospedagem seria em apartamento de luxo e, nos três primeiros dias, a diária custaria R$ 150,00, preço da diária fora da promoção. Nos três dias seguintes, seria aplicada uma redução no valor da diária, cuja taxa média de variação, a cada dia, seria de R$ 20,00. Nos dois dias restantes, seria mantido o preço do sexto dia. Nessas condições, um modelo para a promoção idealizada é apresentado no gráfico a seguir, no qual o valor da diária é função do tempo medido em número de dias.
Uma pousada oferece pacotes promocionais para atrair casais a se hospedarem por até oito dias.

De acordo com os dados e com o modelo, comparando o preço que um casal pagaria pela hospedagem por sete dias fora da promoção, um casal que adquirir o pacote promocional por oito dias fará uma economia de

  1. R$ 90,00.
  2. R$ 110,00.
  3. R$ 130,00.
  4. R$ 150,00.
  5. R$ 170,00.

Texto para a questão 2

A população mundial está ficando mais velha, os ı́ndices de natalidade diminuı́ram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo. Os números da coluna da direita representam as faixas percentuais. Por exemplo, em 1950 havia 95 milhões de pessoas com 60 anos ou mais nos paı́ses desenvolvidos, número entre 10% e 15% da população total nos paı́ses desenvolvidos. A população mundial está ficando mais velha, os ı́ndices de natalidade diminuı́ram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo.

2. (Enem 2009) Suponha que o modelo exponencial y = 363e 0,03x, em que x = 0 corresponde ao ano 2000, x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a população em milhões de habitantes no ano x, seja usado para estimar essa população com 60 anos ou mais de idade nos paı́ses em desenvolvimento entre 2010 e 2050. Desse modo, considerando e 0,3 = 1, 35, estima-se que a população com 60 anos ou mais estará, em 2030, entre

  1. 490 e 510 milhões.
  2. 550 e 620 milhões.
  3. 780 e 800 milhões.
  4. 810 e 860 milhões.
  5. 870 e 910 milhões.

3. (Enem 2009) A vazão do rio Tietê, em São Paulo, constitui preocupação constante nos perı́odos chuvosos. Em alguns trechos, são construı́das canaletas para controlar o fluxo de água. Uma dessas canaletas, cujo corte vertical determina a forma de um trapézio isósceles, tem as medidas especificadas na figura I. Neste caso, a vazão da água é de 1.050m 3/s. O cálculo da vazão, Q em m3/s, envolve o produto da área A do setor transversal (por onde passa a água), em m2, pela velocidade da água no local, v, em m/s, ou seja, Q = Av.

Planeja-se uma reforma na canaleta, com as dimensões especificadas na figura II, para evitar a ocorrência de enchentes. A vazão do rio Tietê, em São Paulo, constitui preocupação constante nos perı́odos chuvosos. Em alguns trechos, são construı́das canaletas para controlar o fluxo de água.

Na suposição de que a velocidade da água não se alterará, qual a vazão esperada para depois da reforma na canaleta?

  1. 90m 3/s.
  2. 750m 3/s.
  3. 1.050m 3/s.
  4. 1.512m 3/s.
  5. 2.009m 3/s.

4. (Enem 2009) Rotas aéreas são como pontes que ligam cidades, estados ou paı́ses. O mapa a seguir mostra os estados brasileiros e a localização de algumas capitais identificadas pelos números. Considere que a direção seguida por um avião AI que partiu de Brası́lia - DF, sem escalas, para Belém, no Pará, seja um segmento de reta com extremidades em DF e em 4. Rotas aéreas são como pontes que ligam cidades, estados ou paı́ses. O mapa a seguir mostra os estados brasileiros e a localização de algumas capitais identificadas pelos números.

Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção que forma um ângulo de 135o graus no sentido horário com a rota Brası́lia - Belém e pousou em alguma das capitais brasileiras. Ao desembarcar, Carlos fez uma conexão e embarcou em um avião AIII, que seguiu a direção que forma um ângulo reto, no sentido anti-horário, com a direção seguida pelo avião AII ao partir de Brası́lia-DF. Considerando que a direção seguida por um avião é sempre dada pela semirreta com origem na cidade de partida e que passa pela cidade destino do avião, pela descrição dada, o passageiro Carlos fez uma conexão em

  1. Belo Horizonte, e em seguida embarcou para Curitiba.
  2. Belo Horizonte, e em seguida embarcou para Salvador.
  3. Boa Vista, e em seguida embarcou para Porto Velho.
  4. Goiânia, e em seguida embarcou para o Rio de Janeiro.
  5. Goiânia, e em seguida embarcou para Manaus.

5. (Enem 2009) Um experimento consiste em colocar certa quantidade de bolas de vidro idênticas em um copo com água até certo nı́vel e medir o nı́vel da água, conforme ilustrado na figura a seguir. Como resultado do experimento, concluiu-se que o nı́vel da água é função do número de bolas de vidro que são colocadas dentro do copo. Um experimento consiste em colocar certa quantidade de bolas de vidro idênticas em um copo com água até certo nı́vel e medir o nı́vel da água, conforme ilustrado na figura a seguir.

O quadro a seguir mostra alguns resultados do experimento realizado. Um experimento consiste em colocar certa quantidade de bolas de vidro idênticas em um copo com água até certo nı́vel e medir o nı́vel da água, conforme ilustrado na figura a seguir.

Qual a expressão algébrica que permite calcular o nı́vel da água (y) em função do número de bolas (x)?

  1. y = 30x.
  2. y = 25x + 20,2.
  3. y = 1,27x.
  4. y = 0,7x.
  5. y = 0,07x + 6.

6. (Enem 2009) Um posto de combustı́vel vende 10.000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10.200 litros.

Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é

  1. V= 10.000 + 50x − x2.
  2. V= 10.000 + 50x + x2.
  3. V= 15.000 − 50x − x2.
  4. V= 15.000 + 50x − x2.
  5. V= 15.000 − 50x + x2.

7. (Enem 2009) O mapa a seguir representa um bairro de determinada cidade, no qual as flechas indicam o sentido das mãos do tráfego. Sabe-se que esse bairro foi planejado e que cada quadra representada na figura é um terreno quadrado, de lado igual a 200 metros. O mapa a seguir representa um bairro de determinada cidade, no qual as flechas indicam o sentido das mãos do tráfego. Sabe-se que esse bairro foi planejado e que cada quadra representada na figura é um terreno quadrado, de lado igual a 200 metros.

Desconsiderando-se a largura das ruas, qual seria o tempo, em minutos, que um ônibus, em velocidade constante e igual a 40 km/h, partindo do ponto X, demoraria para chegar até o ponto Y?

  1. 25 min.
  2. 15 min.
  3. 2,5 min.
  4. 1,5 min.
  5. 0,15 min.

8. (Enem 2009) Dados da Associação Nacional de Empresas de Transportes Urbanos (ANTU) mostram que o número de passageiros transportados mensalmente nas principais regiões metropolitanas do paı́s vem caindo sistematicamente.

Eram 476,7 milhões de passageiros em 1995, e esse número caiu para 321,9 milhões em abril de 2001. Nesse perı́odo, o tamanho da frota de veı́culos mudou pouco, tendo no final de 2008 praticamente o mesmo tamanho que tinha em 2001.

O gráfico a seguir mostra um ı́ndice de produtividade utilizado pelas empresas do setor, que é a razão entre o total de passageiros transportados por dia e o tamanho da frota de veı́culos.
Dados da Associação Nacional de Empresas de Transportes Urbanos (ANTU) mostram que o número de passageiros transportados mensalmente nas principais regiões metropolitanas do paı́s vem caindo sistematicamente.

Supondo que as frotas totais de veı́culos naquelas regiões metropolitanas em abril de 2001 e em outubro de 2008 eram do mesmo tamanho, os dados do gráfico permitem inferir que o total de passageiros transportados no mês de outubro de 2008 foi aproximadamente igual a

  1. 355 milhões.
  2. 400 milhões.
  3. 426 milhões.
  4. 441 milhões.
  5. 477 milhões.

9. (Enem 2010) Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel. Para ilustrar essa situação, esse casal fez um gráfico relacionando as alturas do filho nas idades consideradas.

Que gráfico melhor representa a altura do filho desse casal em função da idade casal em função da idade?

  1. Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel.
  2. Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel.
  3. Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel.
  4. Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel.
  5. Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptı́vel.

10. (Enem 2010) O gráfico a seguir apresenta o gasto militar dos Estados Unidos, no perı́odo de 1988 a 2006.
O gráfico a seguir apresenta o gasto militar dos Estados Unidos, no perı́odo de 1988 a 2006.

Com base no gráfico, o gasto militar no inı́cio da guerra no Iraque foi de

  1. U$ 4.174.000,00.
  2. U$ 41.740.000,00.
  3. U$ 417.400.000,00.
  4. U$ 41.740.000.000,00.
  5. U$ 417.400.000.000,00

11. (Enem 2010) Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigenrante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir.
Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigenrante para montar figuras, onde cada lado foi representado por um canudo.

Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?

  1. C = 4Q
  2. C = 3Q + 1
  3. C = 4Q - 1
  4. C = Q + 3
  5. C = 4Q - 2

12. (Enem 2010) A figura a seguir é a representação de uma região por meio de curvas de nı́vel, que são curvas fechadas representando a altitude da região, com relação ao nı́vel do mar. As coordenadas estão expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala em tons de cinza desenhada à direita está associada à altitude da região.
A figura a seguir é a representação de uma região por meio de curvas de nı́vel, que são curvas fechadas representando a altitude da região, com relação ao nı́vel do mar.

Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O helicóptero segue o percurso: 0,8oL → 0,5oN → 0, 2oO → 0,1oS → 0,4oN → 0, 3oL

De acordo com as orientações, o helicóptero pousou em um local cuja altitude é

  1. menor ou igual a 200 m.
  2. maior que 200 m e menor ou igual a 400 m.
  3. maior que 400 m e menor ou igual a 600 m.
  4. maior que 600 m e menor ou igual a 800 m.
  5. maior que 800 m.

13. (Enem 2010) O gráfico mostra o número de favelas no municı́pio do Rio de Janeiro entre 1980 e 2004, considerando que a variação nesse número entre os anos considerados é linear.
O gráfico mostra o número de favelas no municı́pio do Rio de Janeiro entre 1980 e 2004, considerando que a variação nesse número entre os anos considerados é linear.

Se o padrão na variação do perı́odo 2004/2010 se mantiver nos próximos 6 anos, e sabendo que o número de favelas em 2010 é 968, então o número de favelas em 2016 será

  1. menor que 1 150.
  2. 218 unidades maior que em 2004.
  3. maior que 1 150 e menor que 1 200.
  4. 177 unidades maior que em 2010.
  5. maior que 1 200.

14. (Enem 2010) Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.

Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado.
Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.

Uma peça deve ser colocada nesse forno quando a temperatura for 48oC e retirada quando a temperatura for 200oC.

O tempo de permanência dessa peça no forno é, em minutos, igual a

  1. 100.
  2. 108.
  3. 128.
  4. 130.
  5. 150.

15. (Enem 2010) Para conseguir chegar a um número recorde de produção de ovos de Páscoa, as empresas brasileiras começam a se planejar para esse perı́odo com um ano de antecedência. o gráfico a seguir mostra o número de ovos de Páscoa produzidos no Brasil no perı́odo de 2005 a 2009.
Para conseguir chegar a um número recorde de produção de ovos de Páscoa, as empresas brasileiras começam a se planejar para esse perı́odo com um ano de antecedência.

De acordo com o gráfico, o biênio que apresentou maior produção acumulada foi

  1. 2004-2005.
  2. 2005-2006.
  3. 2006-2007.
  4. 2007-2008.
  5. 2008-2009.

16. (Enem 2011) Uma indústria fabrica um único tipo de produto e sempre vende tudo o que produz. O custo total para fabricar uma quantidade q de produtos é dado por uma função, simbolizada por CT, enquanto o faturamento que a empresa obtém com a venda da quantidade q também é uma função, simbolizada por FT. O lucro total (LT) obtido pela venda da quantidade q de produtos é dado pela expressão LT(q) = FT(q) − CT(q).

Considerando-se as funções FT(q) = 5q e CT(q) = 2q + 12 como faturamento e custo, qual a quantidade mı́nima de produtos que a indústria terá de fabricar para não ter prejuı́zo?

  1. 0
  2. 1
  3. 3
  4. 4
  5. 5

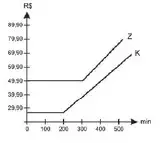
17. (Enem 2011) Uma empresa de telefonia fixa oferece dois planos aos seus clientes: no plano K, o cliente paga R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente; no plano Z paga R$49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.

O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é

  1. O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
  2. O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
  3. O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
  4. O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
  5. O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é

18. (Enem 2011) O termo agronegócio não se refere apenas à agricultura e à pecuária, pois as atividades ligadas a essa produção incluem fornecedores de equipamentos, serviços para a zona rural, industrialização e comercialização dos produtos.

O gráfico seguinte mostra a participação percentual do agronegócio no PIB brasileiro:
O termo agronegócio não se refere apenas à agricultura e à pecuária, pois as atividades ligadas a essa produção incluem fornecedores de equipamentos, serviços para a zona rural, industrialização e comercialização dos produtos.

Esse gráfico foi usado em uma palestra na qual o orador ressaltou uma queda da participação do agronegócio no PIB brasileiro e a posterior recuperação dessa participação, em termos percentuais.

Segundo o gráfico, o perı́odo de queda ocorreu entre os anos de

  1. 1998 e 2001.
  2. 2001 e 2003.
  3. 2003 e 2006.
  4. 2003 e 2007.
  5. 2003 e 2008.

19. (Enem 2011) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.

Disponı́vel em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).

Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano.

Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é

  1. y = 4300x
  2. y = 884905x
  3. y = 872005 + 4300x
  4. y = 876305 + 4300x
  5. y = 880605 + 4300x

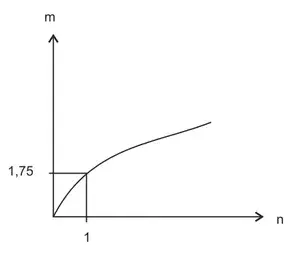
20. ( Enem 2011) As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção. Considere que, independente da época ou variação de preço, certa fruta custa R$ 1,75 o quilograma.

Dos gráficos a seguir, o que representa o preço m pago em reais pela compra de n quilogramas desse produto é

  1. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção.
  2. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção.
  3. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção.
  4. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção.
  5. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção.

Clique Para Compartilhar Esta Página Nas Redes Sociais



Você acredita que o gabarito esteja incorreto? Avisa aí 😰| Email ou WhatsApp

Conheça nossos grupos no WhatsApp