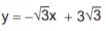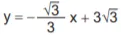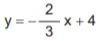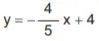Geometria Analı́tica II
Lista de 23 exercícios de Matemática com gabarito sobre o tema Geometria Analı́tica II (Plano, Reta e Circunferência) com questões do Enem.
01. (Enem 2017) O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade V de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a) (v + b) = K, com a, b e K constantes.
Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:
| TIPO DE CURVA |
|---|
| Semirreta oblíqua |
| Semirreta horizontal |
| Ramo de parábola |
| Arco de circunferência |
| Ramo de hipérbole |
O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p. V). Admita que K > 0.
Disponível em: http://rspb.royalsocietypublishing.org. Acesso em: 14jul2015 (adaptado).
O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo
- Semirreta oblíqua.
- semirreta horizontal.
- ramo de parábola.
- arco de circunferência.
- ramo de hipérbole.
02. (Enem 2016) Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
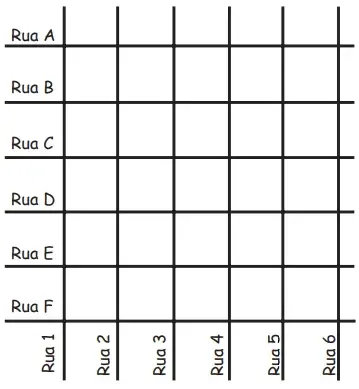
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
- 3 e C
- 4 e C
- 4 e D
- 4 e E
- 5 e C
03. (Enem PPL 2015) Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.
A seguir há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.
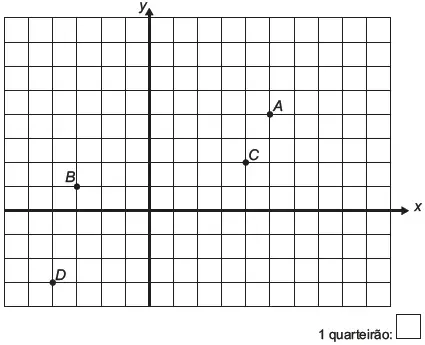
Suponha que uma rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontre num ponto cujas coordenadas satisfaçam à inequação: x² + y² – 2x – 4y – 31 ≤ 0.
A fim de avaliar a qualidade do sinal, e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio enquanto os outros não.
Os estabelecimentos que conseguem ouvir a rádio são apenas
- A e C.
- B e C.
- B e D.
- A, B e C.
- B, C e D.
04. (Enem 2016) Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.

Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
- diminuir em 2 unidades
- diminuir em 4 unidades
- aumentar em 2 unidades.
- aumentar em 4 unidades.
- aumentar em 8 unidades.
05. (Enem 2016) Uma região de uma fábrica deve ser isolada, pois nela os empregados ficam expostos a riscos de acidentes. Essa região está representada pela porção de cor cinza (quadrilátero de área S) na figura.
Para que os funcionários sejam orientados sobre a localização da área isolada, cartazes informativos serão afixados por toda fábrica. Para confeccioná-los, um programador utilizará um software que permite desenhar essa região a partir de um conjunto de desigualdades algébricas.
As desigualdades que devem ser utilizadas no referido software, para o desenho da região de isolamento, são
- 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 8; x ≤ 9
- 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 9; x ≤ 8
- 3y – x ≥ 0; 2y – x ≤ 0; y ≤ 9; x ≤ 8
- 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 8; x ≤ 9
- 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 9; x ≤ 8
06. (Enem 2015) A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.
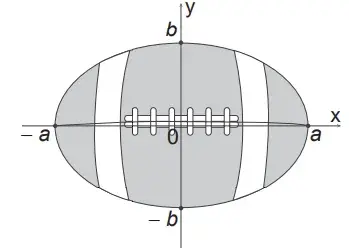
Considere que o volume aproximado dessa bola é dado por V = 4ab².
O volume dessa bola, em função apenas de b, é dado por
- 8b³
- 6b³
- 5b³
- 4b³
- 2b³
07. (Enem 2015) Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
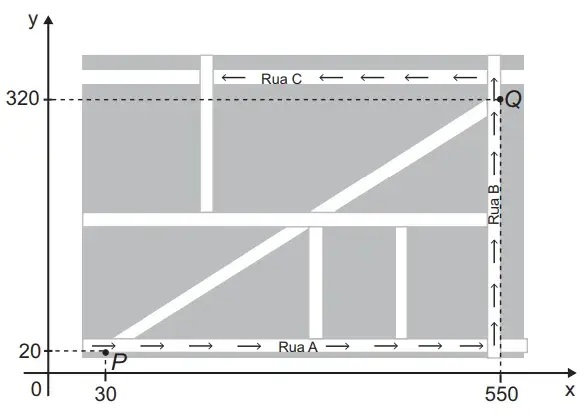
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto de parada são
- (290 ; 20).
- (410 ; 0).
- (410 ; 20).
- (440 ; 0).
- (440 ; 20).
08. (Enem 2009) Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d≤ sobre a circunferência.

Então, o ponto Q percorrerá, no eixo x, uma distância dada por
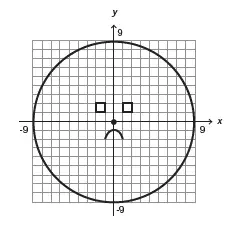
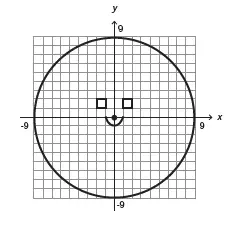
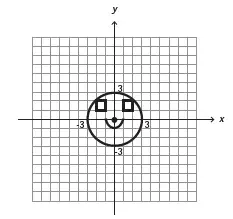
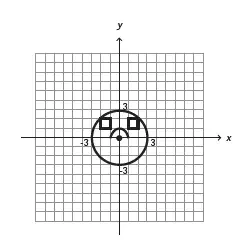
09. (Enem 2013) Durante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:
(I) é a circunferência de equação x² + y² = 9;
(II) é a parábola de equação y = −x² − 1, com x variando de -1 a 1;
(III) é o quadrado formado pelos vértices (-2, 1), (-1, 1), (-1, 2) e (-2, 2);
(IV) é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
(V) é o ponto (0, 0).
A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura. Qual destas figuras foi desenhada pelo professor?
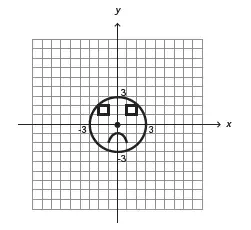
10. (Enem 2016) Na figura estão representadas, em um plano cartesiano, duas circunferências: C1, (de raio 3 e centro O1,) e C2 (de raio 1 e centro O2), tangentes entre si, e uma reta t tangente às duas circunferências nos pontos P e Q.
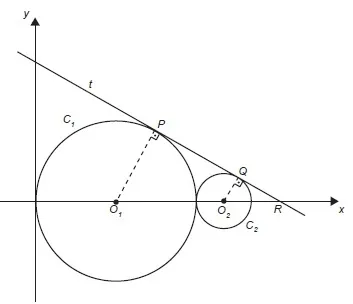
Nessas condições, a equação da reta t é
-
![]()
-
![]()
- y = −x + 4
-
![]()
-
![]()
11. (Enem PPL 2016) Em sua vez de jogar, um jogador precisa dar uma tacada na bola branca, de forma a acertar a bola 9 e fazê-Ia cair em uma das caçapas de uma mesa de bilhar. Como a bola 8 encontra-se entre a bola branca e a bola 9, esse jogador adota a estratégia de dar uma tacada na bola branca em direção a uma das laterais da mesa, de forma que, ao rebater, eIa saia em uma trajetória retilínea, formando um ângulo de 90º com a trajetória da tacada, conforme ilustrado na figura.

Com essa estratégia, o jogador conseguiu encaçapar a bola 9. Considere um sistema cartesiano de eixos sobre o plano da mesa, no qual o ponto de contato da bola com a mesa define sua posição nesse sistema. As coordenadas do ponto que representa a bola 9 são (3 ; 3), o centro da caçapa de destino tem coordenadas (6 ; O) e a abscissa da bola branca e 0,5, como representados na figura. Se a estratégia deu certo, a ordenada da posição original da bola branca era
- 1,3.
- 1,5.
- 1.
- 2,2.
- 2,5.
12. (Enem PPL 2016) Na figura estão representadas três retas no plano cartesiano, sendo P, Q e R os pontos de intersecções entre as retas, e A, B e C os pontos de intersecções dessas retas com o eixo x.

Essa figura é a representação gráfica de um sistema linear de três equações e duas incógnitas que
- possui três soluções reais e distintas, representadas pelos pontos P, Q e R, pois eles indicam onde as retas se intersectam.
- possui três soluções reais e distintas, representadas pelos pontos A, B e C, pois eles indicam onde as retas intersectam o eixo das abscissas.
- possui infinitas soluções reais, pois as retas se intersectam em mais de um ponto.
- não possui solução real, pois não há ponto que pertença simultaneamente às três retas.
- possui uma única solução real, pois as retas possuem pontos em que se intersectam.
13. (Enem 2016) Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B). Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferênciaque contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro.
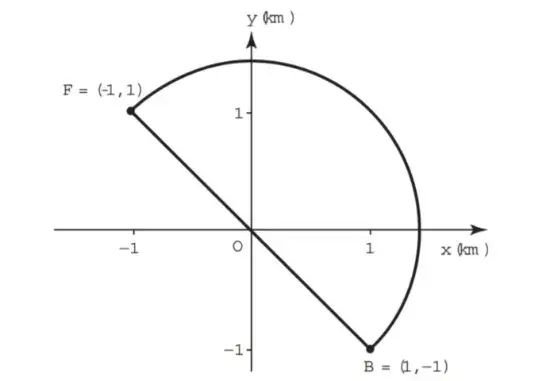
Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro. Use 3 como aproximação para Π; e 1,4 como aproximação para √2 . O menor tempo possível, em hora, para conclusão daconstrução da galeria, para atender às necessidades de água do bairro, é de
- 1 260.
- 2 520.
- 2 800.
- 3 600.
- 4 000.
14. (Enem PPL 2014) Um construtor pretende murar um terreno e, para isso, precisa calcular o seu perímetro. O terreno está representado no plano cartesiano, conforme a figura, no qual foi usada a escala 1 : 500. Use 2,8 como aproximação para √8 .
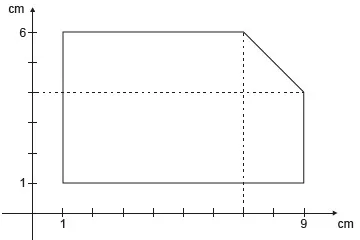
De acordo com essas informações, o perímetro do terreno, em metros, é
- 110.
- 120.
- 124.
- 130.
- 144.
15. (Enem 2014) A figura mostra uma criança brincando em um balanço no parque. A corda que prende o assento do balanço ao topo do suporte mede 2 metros. A criança toma cuidado para não sofrer um acidente, então se balança de modo que a corda não chegue a alcançar a posição horizontal.

Na figura, considere o plano cartesiano que contém a trajetória do assento do balanço, no qual a origem está localizada no topo do suporte do balanço, o eixo X é paralelo ao chão do parque, e o eixo Y tem orientação positiva para cima. A curva determinada pela trajetória do assento do balanço é parte do gráfico da função.
16. (Enem 2013) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
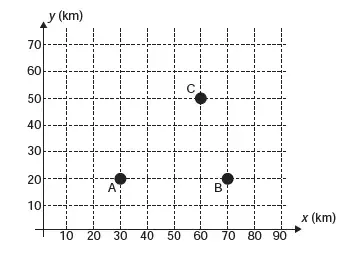
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
- (65 ; 35)
- (53 ; 30)
- (45 ; 35)
- (50 ; 20)
- (50 ; 30)
17. (Enem PPL 2011) No labirinto em um parque de diversões, representado pela malha quadriculada, encontram-se sete crianças: Ana, Carol, Samanta, Denise, Roberta, Eliana e Larissa, representadas por pontos, identificados pela letra inicial do nome de cada uma delas. A malha é formada por quadrados, cujos lados medem 1 cm.
Considere que cada criança pode se deslocar apenas na direção vertical ou horizontal dentro do labirinto. Desse modo, Ana encontra-se equidistante de Samanta e de
- Carol.
- Denise.
- Eliana.
- Larissa.
- Roberta.
18. (Enem PPL 2010) Um foguete foi lançado do marco zero de uma estação e após alguns segundos atingiu a posição (6, 6, 7) no espaço, conforme mostra a figura. As distâncias são medidas em quilômetros.

Considerando que o foguete continuou sua trajetória, mas se deslocou 2 km para frente na direção do eixo-x, 3 km para trás na direção do eixo-y, e 11 km para frente, na direção do eixo-z, então o foguete atingiu a posição
- (17, 3, 9).
- (8, 3, 18).
- (6, 18, 3).
- (4, 9, - 4).
- (3, 8, 18).
19. (Enem PPL 2009) O gráfico a seguir mostra o início da trajetória de um robô que parte do ponto A (2, 0), movimentando-se para cima ou para a direita, com velocidade de uma unidade de comprimento por segundo no plano cartesiano. O gráfico exemplifica uma trajetória desse robô, durante 6 segundos.
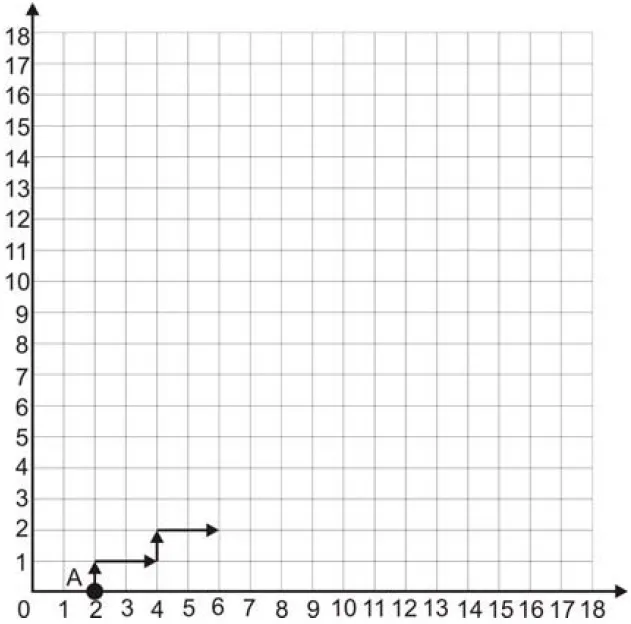
Supondo que esse robô continue essa mesma trajetória, qual será sua coordenada após 18 segundos de caminhada, contando o tempo a partir do ponto A?
- (0, 18)
- (18, 2)
- (18, 0)
- (14, 6)
- (6, 14)
20. (Enem 2011) Um administrador de um campo de futebol deseja recobri-lo com um tipo de grama que, em condições normais, cresce de acordo com o gráfico a seguir.
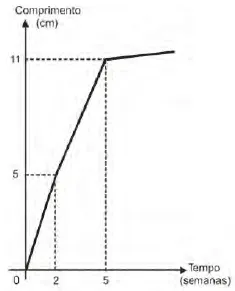
Ele precisa ter o campo pronto no dia 11 de junho de 2012, e o comprimento mínimo da grama nesse dia deve ser igual a 7 cm. Supondo-se que o crescimento da grama se dê em condições normais, a grama deve ser plantada, no máximo, até o dia
- 17 de maio de 2012.
- 21 de maio de 2012.
- 23 de maio de 2012.
- 8 de junho de 2012.
- 9 de junho de 2012.
21. (Enem 2011) Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.

A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade. No ponto P = (-5, 5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km. Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto
- (–5, 0).
- (–3, 1).
- (–2, 1).
- (0, 4).
- (2, 6).
22. (Enem 2010) A figura a seguir é a representação de uma região por meio de curvas de nível, que são curvas fechadas representando a altitude da região, com relação ao nível do mar. As coordenadas estão expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala em tons de cinza desenhada à direita está associada à altitude da região.
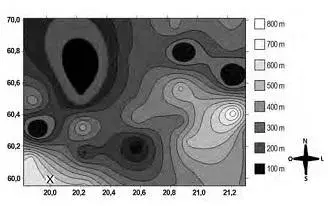
Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O helicóptero segue o percurso: 0,8°L→0,5°N→0,2°O→0,1°S→0,4°N→0,3°L Ao final, desce verticalmente até pousar no solo. De acordo com as orientações, o helicóptero pousou em um local cuja altitude é
- menor ou igual a 200 m.
- maior que 200 m e menor ou igual a 400 m.
- maior que 400 m e menor ou igual a 600 m.
- maior que 600 m e menor ou igual a 800 m.
- maior que 800 m.
23. (Enem 2009) Rotas aéreas são como pontes que ligam cidades, estados ou países. O mapa a seguir mostra os estados brasileiros e a localização de algumas capitais identificadas pelos números. Considere que a direção seguida por um avião AI que partiu de Brasília – DF, sem escalas, para Belém, no Pará, seja um segmento de reta com extremidades em DF e em 4.

Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção que forma um ângulo de 135º graus no sentido horário com a rota Brasília – Belém e pousou em alguma das capitais brasileiras. Ao desembarcar, Carlos fez uma conexão e embarcou em um avião AIII, que seguiu a direção que forma um ângulo reto, no sentido anti-horário, com a direção seguida pelo avião AII ao partir de Brasília-DF. Considerando que a direção seguida por um avião é sempre dada pela semirreta com origem na cidade de partida e que passa pela cidade destino do avião, pela descrição dada, o passageiro Carlos fez uma conexão em
- Belo Horizonte, e em seguida embarcou para Curitiba.
- Belo Horizonte, e em seguida embarcou para Salvador.
- Boa Vista, e em seguida embarcou para Porto Velho.
- Goiânia, e em seguida embarcou para o Rio de Janeiro.
- Goiânia, e em seguida embarcou para Manaus.
| Gabarito |
|---|
| 01.E | 02.C | 03.D | 04.C | 05.E |
| 06.B | 07.E | 08.B | 09.E | 10.B |
| 11.E | 12.D | 13.B | 14.C | 15.D |
| 16.E | 17.B | 18.B | 19.D | 20.B |
| 21.B | 22.A | 23.B | 24. | 25. |