Função do 2º grau ou Função Quadrática

01. (Enem 2024) Uma criança, utilizando um aplicativo, escreveu uma mensagem para enviar a um amigo. Essa mensagem foi escrita seguindo estas etapas:

Etapas Visor de escrita

A criança seguiu copiando e colando, em cada etapa, o que tinha no visor na etapa imediatamente anterior, até concluir a 20ª etapa. Em seguida, enviou a mensagem.

Qual foi o total de figuras contidas na mensagem enviada?

1. 3 x 2¹⁹
2. 3 x 2²⁰
3. 3 x 2²¹
4. 3 x 2²⁰ - 1
5. 3 x 2²⁰ - 3

02. (Enem 2023) Analisando as vendas de uma empresa, o gerente concluiu que o montante arrecadado, em milhar de real, poderia ser calculado pela expressão V(x) = x2/4 - 10x + 105, em que os valores de x representam os dias do mês, variando de 1 a 30.

Um dos fatores para avaliar o desempenho mensal da empresa é verificar qual é o menor montante diário V0 arrecadado ao longo do mês e classificar o desempenho conforme as categorias apresentadas a seguir, em que as quantidades estão expressas em milhar de real.

- Ótimo: V0 ≥ 24

- Bom: 20 ≤ V0 < 24

- Normal: 10 ≤ V0 < 20

- Ruim: 4 ≤ V0 < 10

- Péssimo: V0 < 4

No caso analisado, qual seria a classificação do desempenho da empresa?

1. Ótimo.
2. Bom.
3. Normal.
4. Ruim.
5. Péssimo.

03. (ENEM 2022) Ao analisar os dados de uma epidemia em uma cidade, peritos obtiveram um modelo que avalia a quantidade de pessoas infectadas a cada mês, ao longo de um ano. O modelo é dado por p(t) = -t2 + 10t + 24, sendo t um número natural, variando de 1 a 12, que representa os meses do ano, e p(t) a quantidade de pessoas infectadas no mês t do ano. Para tentar diminuir o número de infectados no próximo ano, a Secretaria Municipal de Saúde decidiu intensificar a propaganda oficial sobre os cuidados com a epidemia. Foram apresentadas cinco propostas (I, II, III, IV e V), com diferentes períodos de intensificação das propagandas:

• I: 1 ≤ t ≤ 2;

• II: 3 ≤ t ≤ 4;

• III: 5 ≤ t ≤ 6;

• IV: 7 ≤ t ≤ 9;

• V: 10 ≤ t ≤ 12.

A sugestão dos peritos é que seja escolhida a proposta cujo período de intensificação da propaganda englobe o mês em que, segundo o modelo, há a maior quantidade de infectados. A sugestão foi aceita.

A proposta escolhida foi a

1. I.
2. II.
3. III.
4. IV.
5. V.

04. (ENEM 2021) Considere que o modelo matemático utilizado no estudo da velocidade V, de uma partícula de um fluido escoando em um tubo, seja diretamente proporcional à diferença dos quadrados do raio R da secção transversal do tubo e da distância x da partícula ao centro da secção que a contém. Isto é, V(x) = K²(R² — x²), em que K é uma constante positiva.

O valor de x, em função de R, para que a velocidade de ,escoamento de uma partícula seja máxima é de

1. 0.
2. R
3. 2R.
4. KR.
5. K2R2.

05. (ENEM 2021) Para a comunicação entre dois navios é utilizado um sistema de codificação com base em valores numéricos. Para isso, são consideradas as operações triângulo Δ e estrela *, definidas sobre o conjunto dos números reais por x Δ y = x² + xy – y² e x * y = xy + x.

O navio que deseja enviar uma mensagem deve fornecer um valor de entrada b, que irá gerar um valor de saída, a ser enviado ao navio receptor, dado pela soma da duas maiores soluções da equação (aΔb)*(bΔa) = 0. Cada valor possível de entrada e saída representa uma mensagem diferente já conhecida pelos dois navios.

Um navio deseja enviar ao outro a mensagem “ATENÇÃO!”. Para isso, deve utilizar o valor de entrada b=1.

Dessa forma, o valor recebido pelo navio receptor será

1. √5
2. √3
3. √1
4. -1+√5/2
5. 3+√5/2

06. (ENEM PPL 2022) A trajetória de uma pessoa que pula de um andaime até o chão é descrita por uma função y = f (x), sendo x e y medidos em metro, conforme mostra a figura.

Seja D o domínio da função f (x), como definida na figura.

Para que a situação representada na figura seja real, o domínio dessa função deve ser igual a

1. {X2}, sendo x2 a raiz positiva de f (x).
2. {X ∈ ℝ | 0 ≤ X ≤ X2}, sendo x2 a raiz positiva de f (x).
3. {X ∈ ℝ | X1 ≤ X ≤ X2}, sendo x1 e x2 raízes de f (x), com x1 < x2.
4. {X ∈ ℝ | X ≥ 0}
5. X ∈ ℝ.

07. (Enem 2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = –2t² + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.

A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.

A segunda dedetização começou no

1. 19º dia.
2. 20º dia.
3. 29º dia.
4. 30º dia.
5. 60º dia.

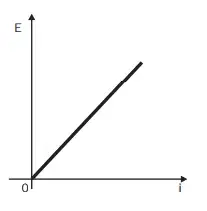
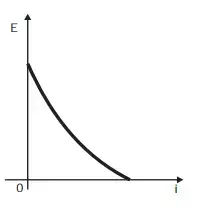
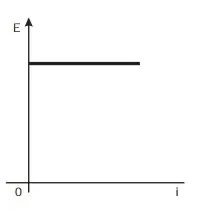
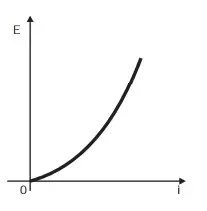
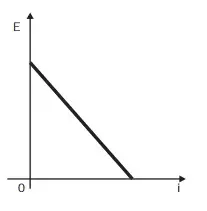
08. (Enem 2012) Existem no mercado chuveiros elétricos de diferentes potências, que representam consumos e custos diversos. A potência (P) de um chuveiro elétrico é dada pelo produto entre sua resistência elétrica (R) e o quadrado da corrente elétrica (i) que por ele circula. O consumo de energia elétrica (E), por sua vez, é diretamente proporcional à potência do aparelho.

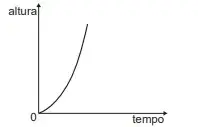
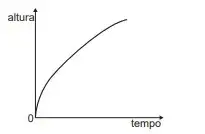
Considerando as características apresentadas, qual dos gráficos a seguir representa a relação entre a energia consumida (E) por um chuveiro elétrico e a corrente elétrica (i) que circula por ele?

09. (Enem 2022) Uma máquina em operação tem sua temperatura T monitorada por meio de um registro gráfico, ao longo do tempo t. Essa máquina possui um pistão cuja velocidade V varia com a temperatura T da máquina, de acordo com a expressão V = T2 - 4. Após a máquina funcionar durante o intervalo de tempo de 10 horas, o seu operador analisa o registro gráfico, apresentado na figura, para avaliar a necessidade de eventuais ajustes, sabendo que a máquina apresenta falhas de funcionamento quando a velocidade do pistão se anula.

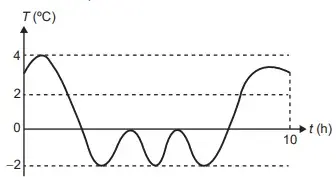
Quantas vezes a velocidade do pistão se anulou durante as 10 horas de funcionamento?

1. 1

2. 2
3. 3
4. 4
5. 5

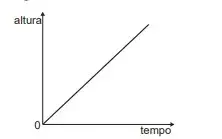
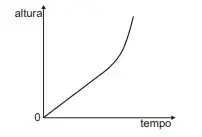
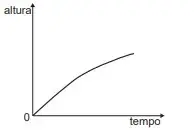
10. (Enem 2020) O consumo de espumantes no Brasil tem aumentado nos últimos anos. Uma das etapas do seu processo de produção consiste no envasamento da bebida em garrafas semelhantes às da imagem. Nesse processo, a vazão do liquido no interior da garrafa é constante e cessa quando atinge o nível de envasamento.

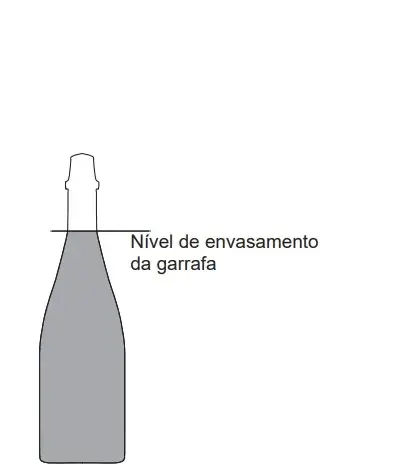
Qual esboço de gráfico melhor representa a variação da altura do liquido em função do tempo, na garrafa indicada na imagem?

11. (Enem 2015) Um estudante está pesquisando o desenvolvimento de certo tipo de bactéria. Para essa pesquisa, ele utiliza uma estufa para armazenar as bactérias. A temperatura no interior dessa estufa, em graus Celsius, é dada pela expressão T(h) = -h2 + 22h - 85, em que h representa as horas do dia. Sabe-se que o número de bactérias é o maior possível quando a estufa atinge sua temperatura máxima e, nesse momento, ele deve retirá-las da estufa.

A tabela associa intervalos de temperatura, em graus Celsius, com as classificações: muito baixa, baixa, média, alta e muito alta.

Quando o estudante obtém o maior número possível de bactérias, a temperatura no interior da estufa está classificada como

1. muito baixa.

2. baixa.
3. média.
4. alta.
5. muito alta.

12. (Enem 2014) A figura mostra uma criança brincando em um balanço no parque. A corda que prende o assento do balanço ao topo do suporte mede 2 metros. A criança toma cuidado para não sofrer um acidente, então se balança de modo que a corda não chegue a alcançar a posição horizontal.

Na figura, considere o plano cartesiano que contém a trajetória do assento do balanço, no qual a origem está localizada no topo do suporte do balanço, o eixo X é paralelo ao chão do parque, e o eixo Y tem orientação positiva para cima.

A curva determinada pela trajetória do assento do balanço é parte do gráfico da função.